Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]

Основные люки (в скобках указаны соответствующие резонансы) располагаются на расстояниях 2,06 а.е. (4:1); 2,50 а.е. (3:1); 2,82 а.е. (5:2); 2,95 а.е. (7:3) и 3,27 а.е. (2:1). Существуют более слабые, или узкие, щели на расстояниях 1,90 а.е. (9:2); 2,25 а.е. (7:2); 2,33 а.е. (10:3); 2,71 а.е. (8:3); 3,03 а.е. (9:4); 3,08 а.е. (11:5); 3,47 а.е. (11:6) и 3,7 а.е. (5:3). Таким образом, именно резонансы управляют распределением больших полуосей орбит астероидов.

Помимо люков, в поясе астероидов имеются уплотнения, известные как группы или кластеры. Опять же, речь, как правило, идет о скоплениях астероидов вблизи некоторого орбитального расстояния, а не об их реальных группах в каких-то конкретных местах. Однако далее мы рассмотрим два настоящих кластера — это ахейцы (греки) и троянцы. Иногда резонансы приводят к образованию не щелей, а скоплений, и зависит это от тех чисел, которыми выражается резонанс, и некоторых других факторов.

Несмотря на то что в общем случае задача трех тел — описать, как движутся три точечные массы под действием гравитации Ньютона, — чрезвычайно тяжело решается математически, кое-какие полезные результаты можно получить, сосредоточившись на особых случаях. Важнейший среди них — это задача «двух с половиной тел», математическая шутка с серьезным смыслом. В этой задаче два тела обладают ненулевыми массами, а третье настолько мало, что его массой можно попросту пренебречь. Примером такой задачи может служить пылинка в поле тяготения Земли и Луны. Основная идея модели заключается в том, что пылинка реагирует на гравитационное воздействие Земли и Луны, но сама она настолько легка, что, по существу, никак не влияет ни на одно, ни на второе тело. Закон всемирного тяготения Ньютона говорит нам, что пылинка все же оказывает влияние, хоть и очень слабое, но влияние это так мало, что при моделировании его можно просто проигнорировать. На практике такой подход работает и с более крупным телом, таким как космический аппарат, небольшая луна или астероид, если промежуток времени, о котором идет речь, достаточно мал, чтобы исключить существенные хаотические эффекты.

В этой модели возможно еще одно упрощение: можно считать, что два крупных тела движутся по круговым орбитам. Это позволяет нам перевести всю задачу во вращающуюся систему отсчета, по отношению к которой большие тела неподвижны и лежат на фиксированной плоскости. Представьте себе большую поворотную площадку. Теперь закрепим Землю и Луну на площадке таким образом, чтобы соединяющая их прямая проходила через центральный шарнир, а сами они располагались от него по разные стороны. Масса Земли примерно в 80 раз превышает массу Луны; если мы поместим Луну в 80 раз дальше от шарнира, чем Землю, то общий центр масс этих двух тел как раз совпадет с шарниром. Далее, если вращать площадку вместе с закрепленными на ней Землей и Луной с правильной скоростью, то планеты будут двигаться по круговым орбитам в полном соответствии с законом всемирного тяготения. При этом в системе координат, связанной с поворотной площадкой, оба тела останутся неподвижны, но будут испытывать на себе эффект вращения в виде «центробежной силы». Это не настоящая физическая сила: она возникает потому, что тела приклеены к площадке и не могут двигаться по прямой. Однако центробежная сила точно так же влияет на динамику тел во вращающейся системе координат, как это делала бы настоящая сила. Ее часто называют «фиктивной силой», несмотря на то, что действие она оказывает самое настоящее.

В 1765 году Эйлер доказал, что в такой модели можно добиться, чтобы все три тела двигались по круговым орбитам в соответствии с законом всемирного тяготения, приклеив пылинку на той же самой прямой, что и два других тела. В этой точке гравитационные силы со стороны Земли и Луны в точности компенсируются центробежной силой, которую испытывает пылинка. Мало того, Эйлер нашел три такие точки. Одна из них (в настоящее время мы называем ее L 1) лежит между Землей и Луной. L 2располагается за Луной, если смотреть на нее с Земли; L 3лежит по ту сторону Земли, если смотреть на нее с Луны.

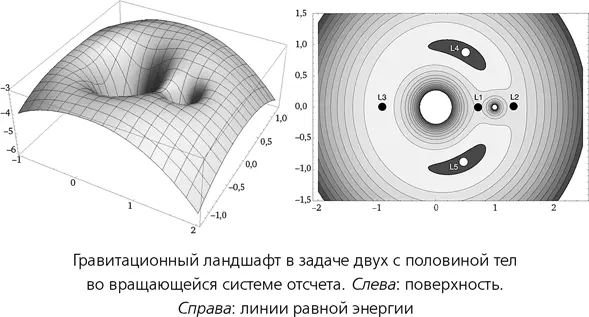
В обозначениях этих точек используется буква L, а не E, как можно было ожидать, потому что в 1772 году Лагранж нашел еще две возможные локации для пылинок. Они лежат не на линии Земля — Луна, а в вершинах двух равносторонних треугольников, двумя другими углами которых являются Земля и Луна. В этих точках пылинка остается неподвижной относительно Земли и Луны. Точка Лагранжа L 4располагается на 60° впереди Луны, а L 5— на 60° позади. Лагранж доказал, что для любых двух тел существует ровно пять таких точек.