Хотя в общем случае мы не можем записать в явном виде решения задачи n тел, существует один класс решений, для которых это может быть сделано, известный как центральные конфигурации. В этих особых состояниях концентрические круги звезд, напоминающие паутину, все вращаются с одной и той же угловой скоростью, как если бы конфигурация была жесткой. Эта идея восходит к работе Джеймса Кларка Максвелла 1859 года о стабильности колец Сатурна, упомянутой в главе 6 в качестве доказательства того, что кольца не могут быть сплошными и твердыми. Саари использует аналогичную идею, чтобы показать, что звездный суп не в состоянии правильно моделировать галактическую динамику.
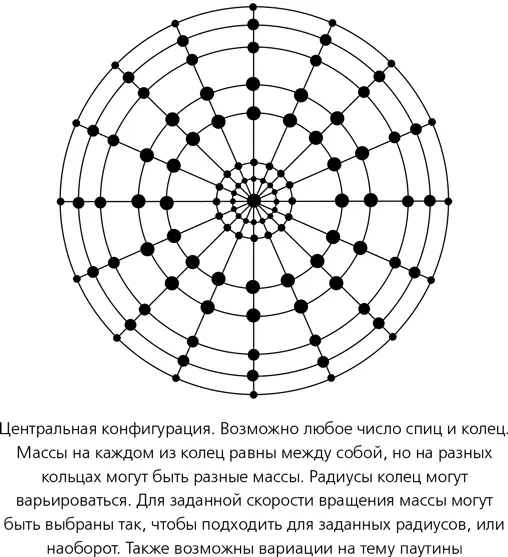
Центральные конфигурации искусственны в том смысле, что никто не станет ожидать такой правильной формы от реальной галактики. С другой стороны, это разумный выбор для исследования того, как сочетаются непрерывная среда и модель n тел. Если выбрать в паутине достаточно радиальных линий и достаточно окружностей, мы получим очень плотный звездный суп, который хорошо аппроксимируется непрерывной средой. Паутинная конфигурация тоже удовлетворяет, с очень хорошим приближением, условиям симметричности, использованным при выводе уравнения Кеплера. Так что аппроксимация типа «звездный суп» должна, по идее, работать.
В частности, для вращающейся паутины должно выполняться уравнение Кеплера. Мы можем это проверить, использовав тот вариант, в котором распределение массы выражается через скорость на заданном радиусе. Поскольку паутина вращается жестко, скорость пропорциональна радиусу. Таким образом, уравнение Кеплера предсказывает распределение масс, пропорциональное кубу радиуса. Такой результат сохраняется, какими бы ни были на самом деле массы звезд в конфигурации.
Чтобы это проверить, мы проведем точный дискретный расчет n тел для паутины. Теория центральных конфигураций допускает значительную гибкость в выборе масс звезд. К примеру, если каждая звезда (а следовательно, каждое кольцо) обладает одинаковой массой, центральные конфигурации существуют, и распределение массы вдоль радиуса всегда меньше чем константа, умноженная на радиус. В данном случае, однако, из уравнения Кеплера может следовать, что масса самого далекого внешнего кольца в миллион раз больше массы внутреннего, даже в том случае, когда на самом деле их массы одинаковы. Так что точные расчеты не оправдывают упрощенную модель, из которой получено уравнение Кеплера. Напротив, по мере увеличения радиуса правильно вычисленная масса растет намного медленнее, чем предсказывает формула Кеплера.
Этот расчет доказывает, что модель в варианте звездного супа может дать результат со значительной ошибкой, даже когда предположения, на которых модель основана, выполняются. Несмотря на популярное выражение, отражающее бытовой, житейский взгляд на вещи, одного исключения достаточно, чтобы опровергнуть любое правило [103] Фраза «Исключение лишь подтверждает правило» используется очень широко, когда нужно избавиться от неудобных исключений. Я никогда не понимал, почему люди это делают — кроме, конечно, желания победить в споре. Это утверждение бессмысленно. Оно восходит к Древнему Риму, к юридическому принципу «exceptio probat regulam in casibus non exceptis» («исключение подтверждает правило в случаях неисключенных»). Это означает, что если у вашего правила есть исключения, то вам нужно другое правило. Это имеет смысл. При современном использовании вторая часть фразы опускается, и получается чепуха.
.
Расчеты Саари имеют еще одно важное следствие. Если темное вещество, как считают астрономы, существует и образует вокруг галактик обширные, массивные гало, то оно не может на самом деле объяснить аномальную кривую вращения, с которой, собственно, все и началось. Либо закон всемирного тяготения, либо традиционные модельные допущения должны быть неверны.
19. За пределами Вселенной
Иногда Создатель Звезд создавал творение, которое, по существу, представляло собой группу из множества связанных вселенных, совершенно отдельных физических систем самых разных типов.
Олаф Стэплдон. «Создатель Звезд»
ДЛЯ ЧЕГО МЫ ЗДЕСЬ?
Это основной вопрос философии. Сквозь окна своих глаз человек смотрит на мир, который гораздо больше и могущественнее его. Даже если единственный известный вам мир — маленькая деревенька на лесной полянке, существуют еще грозы, львы, а иногда приходится мериться силами и с гиппопотамом — и все это грозные противники. Если, как считают сегодня космологи, ваш мир имеет 91 миллиард световых лет в поперечнике и все время увеличивается , это, откровенно говоря, внушает смирение. Вокруг чертовски много «здесь» и очень мало «нас». Поэтому вопрос «для чего?» приобретает поистине катастрофические размеры.
Читать дальше
Конец ознакомительного отрывка
Купить книгу
![Йэн Стюарт Математика космоса [Как современная наука расшифровывает Вселенную] обложка книги](/books/429584/jen-styuart-matematika-kosmosa-kak-sovremennaya-nau-cover.webp)



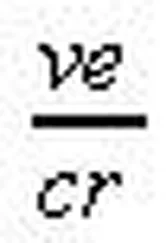
![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]](/books/419776/jen-styuart-ukrochenie-beskonechnosti-istoriya-matema-thumb.webp)



