Оказывается очень удобным ввести вектор k, называемый волновым вектором; величина его равна волновому числу 2π/λ, а направление совпадает с направлением распространения волны
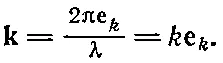 (34.19)
(34.19)
Благодаря введению этого вектора волна приобретает вид cos(ωt- k· r), или cos(ωt-k xx-k yy-k zz). Выясним смысл проекций k, например k x. Очевидно, k xесть скорость изменения фазы в зависимости от координаты х. Фиг 34.11 подсказывает нам, что фаза меняется с ростом х так, как если бы вдоль х бежала волна, но соответствующая ей длина волны оказывается больше по величине. «Длина волны в направлении х» больше истинной на множитель, равный секансу угла α между осью х и направлением движения истинной волны:
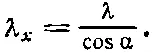 (34.20)
(34.20)
Следовательно, скорость изменения фазы, обратно пропорциональная λ x, в направлении х оказывается меньше на множитель cosα; но этот же множитель содержит и k x, равный модулю k, умноженному на косинус угла между kи осью х!
Итак, мы выяснили смысл волнового вектора, описывающего распространение волны в трехмерном пространстве. Четыре величины ω, k x, k y, k zпреобразуются в теории относительности как четырехвектор, причем ω соответствует времени, а k x, ky, k zсоответствуют x, y и z и компонентам четырехвектора.
Еще раньше, когда мы занимались теорией относительности (гл. 17), мы выяснили, что из четырехвекторов можно составить релятивистское штрихованное произведение. Взяв вектор положения x μ(где μ нумерует четыре компоненты — время и три пространственные) и волновой вектор k μ(где μ снова пробегает четыре значения), образуем штрихованное произведение х μи k μ, записываемое в виде ∑'k μх μ. Это произведение есть инвариант, не зависящий от выбора системы координат. Согласно определению штрихованного произведения, можно записать ∑'k μх μ. следующем виде:
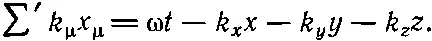 (34.21)
(34.21)
Поскольку k μесть четырехвектор, то, как мы уже знаем, ∑'k μx μесть инвариант по отношению к преобразованиям Лоренца. Под знак косинуса в нашей формуле для плоской волны входит именно это произведение, и оно обязано быть инвариантом относительно преобразований Лоренца. У нас не может появиться формула, у которой под знаком косинуса стоит неинвариантная величина, потому что мы знаем, что значение фазы не зависит от выбора системы координат.
При выводе формул (34.17) и (34.18) мы взяли простой пример, когда kлежит в направлении движения системы координат; но мы можем обобщить теперь эти формулы на другие возможные случаи. Пусть источник посылает луч света в определенном направлении; это направление фиксируется неподвижным наблюдателем, а мы движемся, скажем, по поверхности Земли в горизонтальном направлении (фиг. 34.12,а).
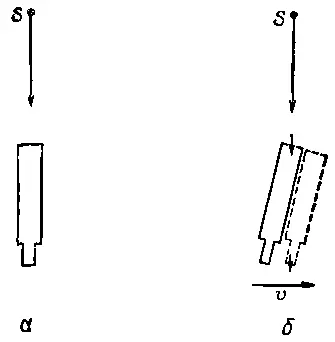
Фиг , 34.12. Удаленный источник света S. а — наблюдаемый через неподвижный телескоп ; б — наблюдаемый через телескоп, движущийся в боковом направлении .
В каком направлении падает луч света с нашей точки зрения? Можно получить ответ, записав четыре компоненты k μи совершив преобразования Лоренца. Но можно воспользоваться и следующим рассуждением: чтобы увидеть луч, следует наш телескоп повернуть на некоторый угол (фиг. 34.12, б). Почему? Потому что свет падает сверху со скоростью с, а мы движемся горизонтально со скоростью v, и свет пройдет «прямо» через телескоп, если последний наклонить на некоторый угол. Легко понять, что расстояние по горизонтали равно vt , а по вертикали ct , и, обозначив угол наклона через θ', мы получим tgθ'=v/c. Замечательно! В самом деле, замечательно, если бы не одна маленькая деталь: θ' не есть тот угол, под которым надо установить телескоп по отношению к поверхности Земли , потому что наш анализ проводился с точки зрения неподвижного наблюдателя.
Горизонтальное расстояние, которое мы считали равным vt , неподвижный по отношению к Земле наблюдатель найдет равным совсем другой величине, так как он пользуется, с нашей точки зрения, «сжатой» линейкой. Из-за эффекта сокращения возникает совсем другое соотношение:
Читать дальше

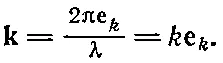 (34.19)
(34.19)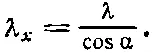 (34.20)
(34.20)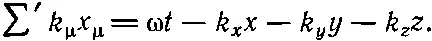 (34.21)
(34.21)





