и, казалось бы, не похоже на (34.12)!
Отличается ли частота, наблюдаемая при нашем движении к источнику, от частоты, наблюдаемой при движении источника к нам? Конечно, нет! Теория относительности утверждает, что обе частоты должны быть в точности равны . Если бы мы были достаточно математически подготовлены, то могли бы убедиться, что оба математических выражения в точности равны! В действительности требование равенства обоих выражений часто используется для вывода релятивистского замедления времени, потому что без квадратных корней равенство сразу нарушается.
Раз уж мы начали говорить о теории относительности, приведем еще и третий способ доказательства, который покажется, пожалуй, более общим. (Суть дела остается прежней, ибо не играет роли, каким способом получен результат!) В теории относительности имеется связь между положением в пространстве и временем, определяемым одним наблюдателем, и положением и временем, определяемым другим наблюдателем, движущимся относительно первого. Мы уже выписывали эти соотношения (гл. 16). Они представляют собой преобразования Лоренца , прямые и обратные:
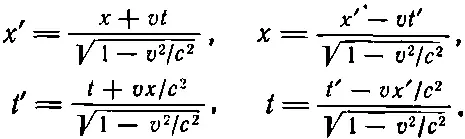 (34.15)
(34.15)
Для неподвижного наблюдателя волна имеет вид cos(ωt- kx ); все гребни, впадины и нули описываются этой формой. А как будет выглядеть та же самая физическая волна для движущегося наблюдателя? Там, где поле равно нулю , любой наблюдатель при измерении получит нуль; это есть релятивистский инвариант. Следовательно, форма волны не меняется, нужно только написать ее в системе отсчета движущегося наблюдателя:
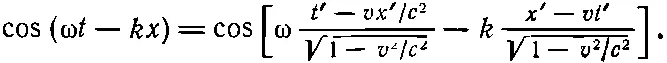
Произведя перегруппировку членов, получим
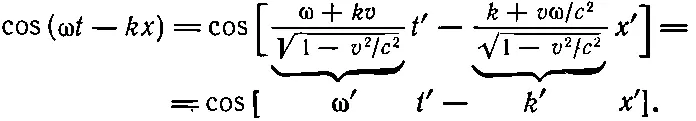 (34.16)
(34.16)
Мы снова получим волну в виде косинуса с частотой ω' в качестве коэффициента при t' и некоторой другой константой k' — коэффициентом при х'. Назовем k' (или число колебаний на 1 м) волновым числом для второго наблюдателя. Таким образом, движущийся наблюдатель отметит другую частоту и другое волновое число, определяемые формулами
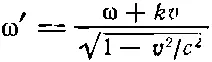 (34.17)
(34.17)
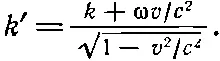 (34.18)
(34.18)
Легко видеть, что (34.17) совпадает с формулой (34.13), полученной нами на основании чисто физических рассуждений.
§ 7. Четырехвектор (ω, k)
Соотношения (34.17) и (34.18) обладают весьма интересным свойством: новая частота ω' линейно связана со старой частотой ω и старым волновым числом k, а новое волновое число представляется в виде комбинации старого волнового числа и частоты. Далее, волновое число есть скорость изменения фазы с расстоянием, а частота — скорость изменения фазы со временем, и сами соотношения обнаруживают глубокую аналогию с преобразованиями Лоренца для координаты и времени: если ω сопоставить с t , а k с х / с 2, то новое ω' сопоставляется с t', a k' — с координатой х '/ с 2. Иначе говоря, при преобразовании Лоренца ω и k изменяются так же, как t и х. Эти величины ω и k составляют так называемый четырехвектор. Четырехкомпонентная величина, преобразующаяся как время и координаты, и есть четырехвектор. Здесь все правильно, за исключением одного — четырехвектор имеет четыре компоненты, а у нас фигурируют только две! Как уже говорилось, ω и k подобны времени и одной координате пространства; для введения двух остальных координат надо изучить распространение света в трехмерном пространстве.
Пусть задана система координат x, y, z и волна движется в пространстве с волновым фронтом (фиг. 34.11). Длина волны есть λ, а направление распространения волны не совпадает ни с одной осью координат.
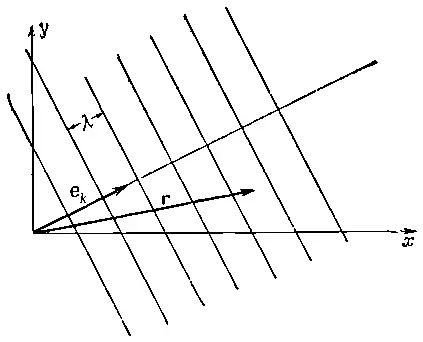
Фиг. 34.11. Плоская волна, движущаяся под углом.
Какой вид имеет формула движения для такой волны? Ответ очевиден: это cos(ωt-ks), где k=2π/ λ a s (расстояние вдоль направления движения волны) — проекция вектора положения на направление движения. Запишем это следующим образом: пусть rесть вектор точки в пространстве, тогда s есть r· е k, где e k— единичный вектор в направлении движения волны. Иначе говоря, s равно rcos( r·e k), проекции расстояния на направление движения. Следовательно, наша волна описывается формулой cos(ωt-k e k· r).
Читать дальше

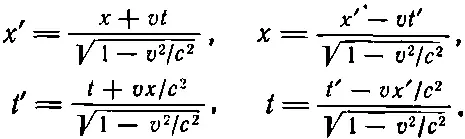 (34.15)
(34.15)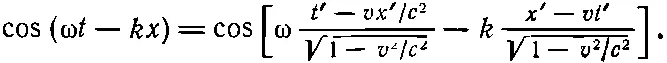
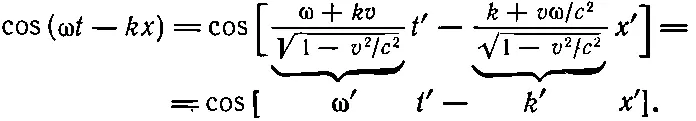 (34.16)
(34.16)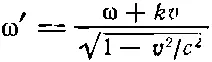 (34.17)
(34.17)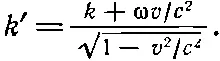 (34.18)
(34.18)





