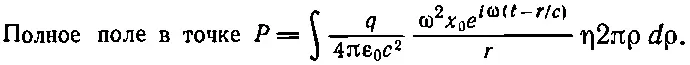
Интеграл берется в пределах ρ=0 и ρ=∞. Время t , конечно, зафиксировано, так что единственными меняющимися величинами являются ρ и r. Отвлечемся пока от постоянных множителей, включая и e i ω t , и вычислим интеграл
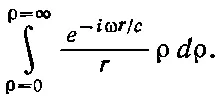 (30.13)
(30.13)
Для этого учтем соотношение между ρ и r:
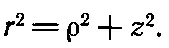 (30.14)
(30.14)
При дифференцировании формулы (30.14) z нужно считать независимым от ρ, тогда
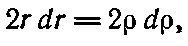
что очень кстати, поскольку при замене в интеграле ρdρ на r dr знаменатель r сокращается. Интеграл приобретает более простой вид
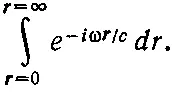 (30.15)
(30.15)
Экспонента интегрируется очень просто. Нужно поставить в знаменатель коэффициент при r в показателе экспоненты и взять саму экспоненту в точках, соответствующих пределам. Но пределы по r отличаются от пределов по ρ. Когда ρ=0, нижний предел r=z, т. е. пределы по r равны z и бесконечности. Интеграл (30.15) равен
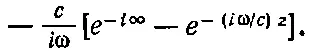 (30.16)
(30.16)
Вместо (r/с)∞ мы здесь написали ∞, поскольку и то и другое означает просто сколь угодно большую величину!
А вот е - i ∞— величина загадочная. Ее действительная часть, равная cos(-∞), с математической точки зрения величина совершенно неопределенная. [Хотя можно допустить, что она находится где-то [а может быть и всюду (?)—между +1 и -1!]Но в физической ситуации эта величина может означать нечто вполне разумное и обычно оказывается равной нулю. Чтобы убедиться, что это так в нашем случае, вернемся к первоначальному интегралу (30.15)
Выражение (30.15) можно понимать как сумму большого числа маленьких комплексных чисел, модуль которых Δr, а угол в комплексной плоскости θ=-ωr/с. Попробуем оценить эту сумму графически. На фиг. 30.11 отложены первые пять членов суммы. Каждый отрезок кривой имеет длину Δr и расположен под углом Δθ=-ω(Δr/ с ) к предыдущему отрезку. Сумма первых пяти слагаемых обозначена стрелкой из начальной точки к концу пятого отрезка. Продолжая прибавлять отрезки, мы опишем многоугольник, вернемся примерно к начальной точке и начнем описывать новый многоугольник. Чем большее число отрезков мы будем прибавлять, тем большее число раз мы обернемся, двигаясь почти по окружности с радиусом с/. Теперь понятно, почему интеграл дает при вычислении неопределенный ответ!
Здесь мы должны обратиться к физическому смыслу нашего примера. В любой реальной ситуации плоскость зарядов не может быть бесконечной, а должна где-то оборваться. Если плоскость резко обрывается и ее граница имеет точно форму окружности, то наш интеграл будет равен некоторому значению на этой окружности (см. фиг. 30.11).
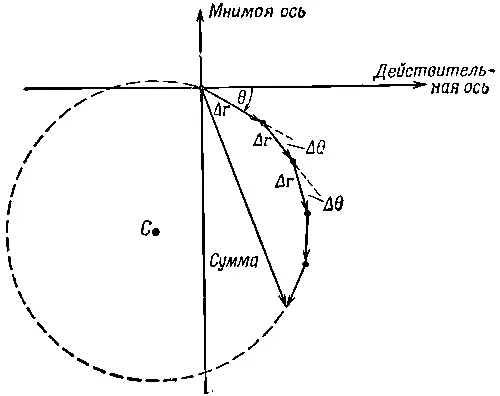
Фиг. 30.11. Вычисление интеграла z ∫∞e -iωr/c dr графическим способом; θ=—ωr/c; Δθ=—ωΔr/c;
Если же плотность зарядов постепенно уменьшается по мере удаления от центра (или обращается в нуль вне некоторой границы неправильной формы, так что для достаточно больших ρ вклад всего кольца шириной dρ равен нулю), то коэффициент η в точном интеграле убывает, стремясь к нулю. Поскольку длина добавляемых отрезков в этом случае уменьшается, а угол Δθ остается тем же самым, график кривой, соответствующей интегралу, будет иметь вид спирали. Спираль оканчивается в центре первоначальной окружности, как изображено на фиг. 30.12.
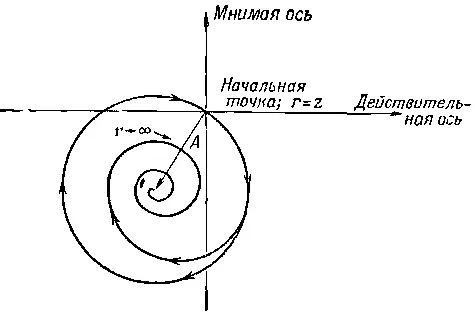
Фиг. 30.12. Вычисление интеграла z ∫∞ηe -iωr/c dr графическим способом,
Физически правильное значение интеграла дается величиной А , которой на схеме соответствует расстояние от начальной точки до центра окружности, равное как нетрудно убедиться
Читать дальше

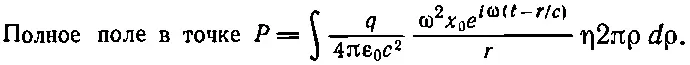
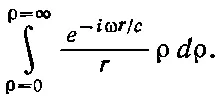 (30.13)
(30.13)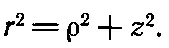 (30.14)
(30.14)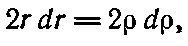
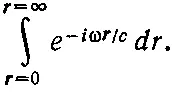 (30.15)
(30.15)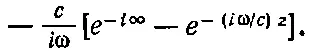 (30.16)
(30.16)






