Второй элемент цепи называется сопротивлением ; этот элемент оказывает сопротивление текущему через него электрическому току. Оказывается, что все металлические провода, а также многие другие материалы сопротивляются току одинаково; если к концам куска такого материала приложить разность потенциалов, то электрический ток в куске I = dq / dt будет пропорционален приложенной разности потенциалов
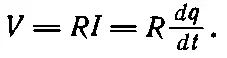 (23.15)
(23.15)
Коэффициент пропорциональности называют сопротивлением R . Соотношение между током и разностью потенциалов вам, наверное, уже известно. Это закон Ома.
Если представлять себе заряд, сосредоточенный в емкости, как нечто аналогичное смещению механической системы х , то электрический ток dq / dt аналогичен скорости, сопротивление R аналогично коэффициенту сопротивления c , а 1/С аналогично постоянной упругости пружины k . Самое интересное во всем этом, что существует элемент цепи, аналогичный массе ! Это спираль, порождающая внутри себя магнитное поле, когда через нее проходит ток. Изменение магнитного поля порождает на концах спирали разность потенциалов, пропорциональную dI / dt . (Это свойство спирали используется в трансформаторах.) Магнитное поле пропорционально току, а наведенная разность потенциалов (так ее называют) пропорциональна скорости изменения тока
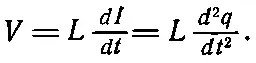 (23.16)
(23.16)
Коэффициент L — это коэффициент самоиндукции ; он является электрическим аналогом массы.
Предположим, мы собираем цепь из трех последовательно соединенных элементов (фиг. 23.5); приложенная между точками 1 и 2 разность потенциалов заставит заряды двигаться по цепи, тогда на концах каждого элемента цепи тоже возникает разность потенциалов: на концах индуктивности V L = L ( d 2 q / dt 2), на сопротивлении V R = R ( dq / dt ), а на емкости V c = q / C .
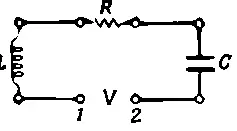
Фиг. 23.5. Электрический колебательный контур, состоящий из сопротивления, индуктивности и емкости.
Сумма этих напряжений дает нам полное напряжение
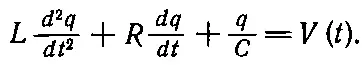 (23.17)
(23.17)
Мы видим, что это уравнение в точности совпадает с механическим уравнением (23.6); будем решать его точно таким же способом. Предположим, что V ( t ) осциллирует; для этого надо соединить цепь с генератором синусоидальных колебаний. Тогда можно представить V ( t ) как комплексное число V , помня, что для определения настоящего напряжения V ( t ) это число надо еще умножить на exp ( i ω t ) и взять действительную часть. Аналогично можно подойти и к заряду q , а поэтому напишем уравнение, в точности повторяющее (23.8): вторая производная ^q— это (iω) 2^q, а первая — это ( i ω)^ q . Уравнение (23.17) перейдет в
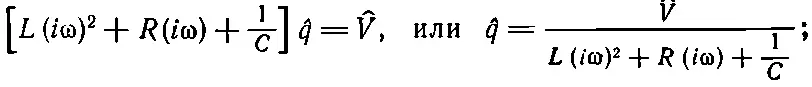
последнее равенство запишем в виде
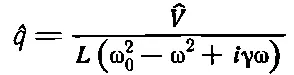 (23.18)
(23.18)
где ω 2 0=1/ LC , а γ= R / L . Мы получили тот же знаменатель, что и в механической задаче, со всеми его резонансными свойствами! В табл. 23.1 приведен перечень аналогий между электрическими и механическими величинами.
Таблица 23.1 МЕХАНИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ВЕЛИЧИНЫ

Еще одно чисто техническое замечание. В книгах по электричеству используют другие обозначения. (Очень часто в книгах на одну и ту же тему, написанных людьми разных специальностей, используются различные обозначения.) Во-первых, для обозначения √-1 используют букву j , а не i (через i должен обозначаться ток!). Во-вторых, инженеры предпочитают соотношение между ^ V и ^ I , а не между ^ V и ^ q . Они так больше привыкли. Поскольку ^I= d ^ q / dt = i ω^ q , то вместо ^ q можно подставить ^ I /iω, и тогда
Читать дальше

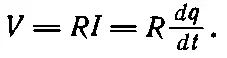 (23.15)
(23.15)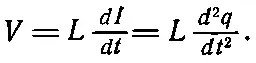 (23.16)
(23.16)
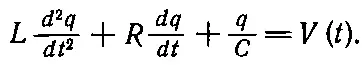 (23.17)
(23.17)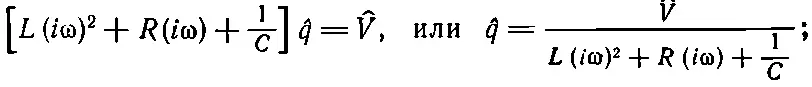
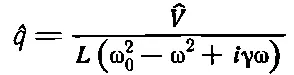 (23.18)
(23.18)





