Итак, уравнения для энергии и импульса имеют вид
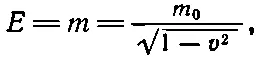
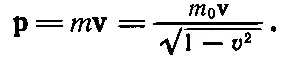 (17.6)
(17.6)
Значит, при таком выборе единиц получится
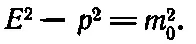 (17.7)
(17.7)
Скажем, если энергия выражена в электронвольтах (эв), то чему равна масса в 1 эв? Она равна массе с энергией покоя 1 эв , т. е. m 0c 2=1 эв . У электрона, например, масса покоя равна 0,511·10 6 эв .
Как же будут выглядеть импульс и энергия в новой системе координат? Чтобы узнать это, надо преобразовать уравнения (17.6). Это преобразование легко получить, зная, как преобразуется скорость. Пусть некоторое тело имело скорость v , а мы наблюдаем за ним из космического корабля, который сам имеет скорость u , и обозначаем соответствующие величины штрихами. Для простоты сперва мы рассмотрим случай, когда скорость v направлена по скорости u . (Более общий случай мы рассмотрим позже.) Чему равна скорость тела v ' по измерениям из космического корабля? Эта скорость равна «разности» между v и u . По прежде полученному нами закону
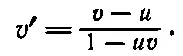 (17.8)
(17.8)
Теперь подсчитаем, какой окажется энергия Е ' по измерениям космонавта. Он, конечно, воспользуется той же массой покоя, но зато скорость станет v '. Он возведет v ' в квадрат, вычтет из единицы, извлечет квадратный корень и найдет обратную величину
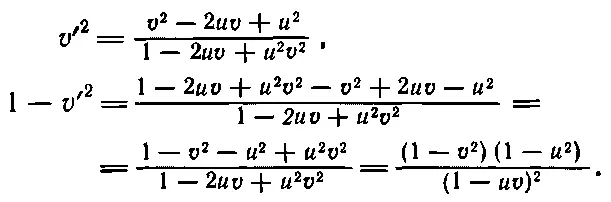
Поэтому
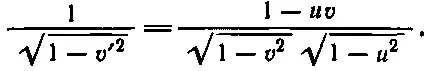 (17.9)
(17.9)
Энергия Е ' просто равна массе m 0, умноженной на это выражение. Но нам хочется выразить энергию через нештрихованные энергию и импульс. Мы замечаем, что
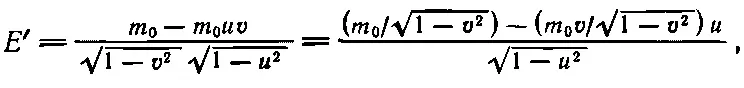
или
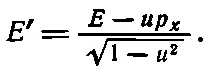 (17.10)
(17.10)
Мы узнаем в этом выражении знакомое нам преобразование
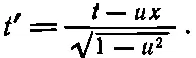
Теперь мы должны найти новый импульс р ' x . Он равен энергии Е ', умноженной на v ', и так же просто выражается через Е и р :
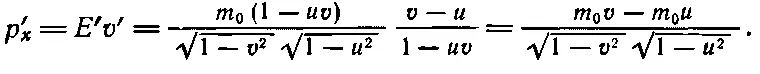
Итак,
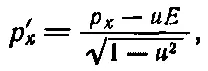 (17.11)
(17.11)
и мы опять распознаем в этой формуле знакомое нам
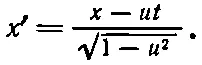
Итак, преобразование старых энергии и импульса в новые энергию и импульс в точности совпало с преобразованием t и х в t ' и х и t в х ': если мы в уравнениях (17.4) будем писать Е каждый раз, когда увидим t , а вместо x: всякий раз будем подставлять р x , то уравнения (17.4) превратятся в уравнения (17.10) и (17.11). Если все верно, то это правило предполагает добавочные равенства р ' у =- р y и р ' z = р z . Чтобы их доказать, надо посмотреть, как преобразуется движение вверх или вниз. Но как раз в предыдущей главе мы рассмотрели такое движение. Мы анализировали сложное столкновение и заметили, что поперечный импульс действительно не меняется при переходе в движущуюся систему координат. Стало быть, мы уже убедились, что р ' у = р у и p z = p z . Итак, полное преобразование равно
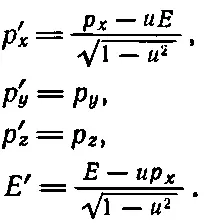 (17.12)
(17.12)
Таким образом, эти преобразования выявили четыре величины, которые преобразуются подобно x, y, z, t . Назовем их четырехвектор импульса . Так как импульс — это четырехвектор, его можно изобразить на диаграмме пространства-времени движущейся частицы в виде «стрелки», касательной к пути (фиг. 17.4).
Читать дальше

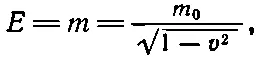
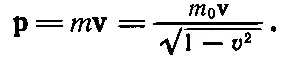 (17.6)
(17.6)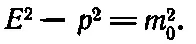 (17.7)
(17.7)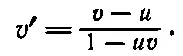 (17.8)
(17.8)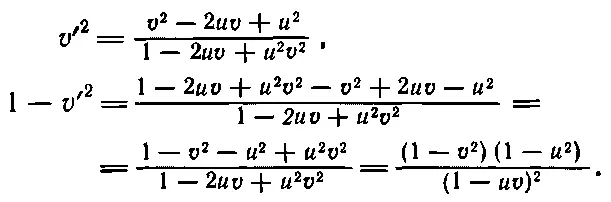
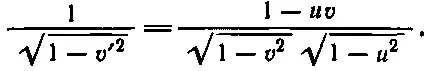 (17.9)
(17.9)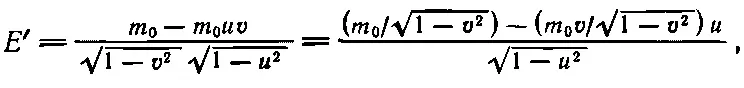
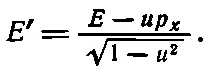 (17.10)
(17.10)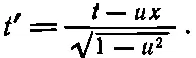
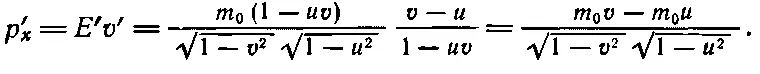
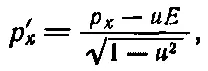 (17.11)
(17.11)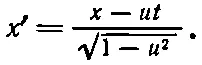
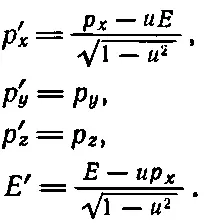 (17.12)
(17.12)




