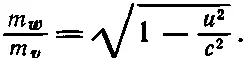 (16.9).
(16.9).
Перейдем к предельному случаю, когда w стремится к нулю. При очень малых w величины v и u практически совпадут, m w → m 0, а m v → m u . Окончательный результат таков:
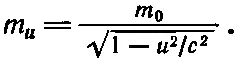 (16.10)
(16.10)
Проделайте теперь такое интересное упражнение: проверьте, будет ли выполнено условие (16.9) при произвольных w, когда масса подчиняется формуле (16.10). При этом скорость v , стоящую в уравнении (16.9), можно найти из прямоугольного треугольника
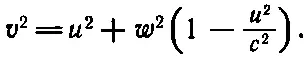
Вы увидите, что (16.9) выполняется тождественно, хотя выше нам понадобился только предел этого равенства при w →0. Теперь перейдем к дальнейшим следствиям, считая уже, что, согласно (16.10), масса зависит от скорости. Рассмотрим так называемое неупругое столкновение . Для простоты предположим, что из двух одинаковых тел, сталкивающихся с равными скоростями w , образуется новое тело, которое больше не распадается (фиг. 16.4,а).
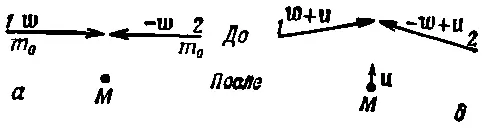
Фиг. 16.4. Две картины неупругого соударения тел равной массы.
Массы тел до столкновения равны, как мы знаем, m 0/√(1- w 2/ c 2). Предположив сохраняемость импульса и приняв принцип относительности, можно продемонстрировать интересное свойство массы вновь образованного тела. Представим себе бесконечно малую скорость u , поперечную к скоростям w (можно было бы работать и с конечной скоростью и , но с бесконечно малым значением и легче во всем разобраться), и посмотрим на это столкновение, двигаясь в лифте со скоростью - u . Перед нами окажется картина, изображенная на фиг. 16.4, а. Составное тело обладает неизвестной массой М . У тела 1, как и у тела 2, есть компонента скорости и , направленная вверх, и горизонтальная компонента, практически равная w . После столкновения остается масса М , движущаяся вверх со скоростью u , много меньшей и скорости света и скорости w . Импульс должен остаться прежним; посмотрим поэтому, каким он был до столкновения и каким стал потом. До столкновения он был равен p ~=2 m w u, а потом стал р '= M u u . Но M u из-за малости u, по существу, совпадает с М 0. Благодаря сохранению импульса
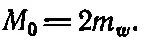 (16.11)
(16.11)
Итак, масса тела, образуемого при столкновении двух одинаковых тел, равна их удвоенной массе . Вы, правда, можете сказать: «Ну и что ж, это просто сохранение массы». Но не торопитесь восклицать: «Ну и что ж!», потому что сами - то массы тел были больше, чем когда тела неподвижны . Они вносят в суммарную массу М не массу покоя, а больше . Не правда ли, поразительно! Оказывается, сохранение импульса в столкновении двух тел требует, чтобы образуемая ими масса была больше их масс покоя, хотя после столкновения эти тела сами придут в состояние покоя!
§ 5. Релятивистская энергия
Немного выше мы показали, что зависимость массы от скорости и законы Ньютона приводят к тому, что изменения в кинетической энергии тела, появляющиеся в результате работы приложенных к нему сил, оказываются всегда равными
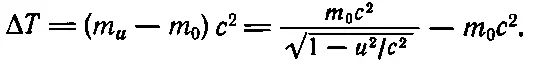 (16.12)
(16.12)
Потом мы продвинулись дальше и обнаружили, что полная энергия тела равна полной его массе, умноженной на с 2. Продолжим эти рассуждения.
Предположим, что наши два тела с равными массами (те, которые столкнулись) можно «видеть» даже тогда, когда они оказываются внутри тела М . Скажем, протон с нейтроном столкнулись, но все еще продолжают двигаться внутри М . Масса тела М , как мы обнаружили, равна не 2 m 0, а 2 m w . Этой массой 2 m w снабдили тело его составные части, чья масса покоя была 2m 0; значит, избыток массы составного тела равен привнесенной кинетической энергии. Это означает, конечно, что у энергии есть инерция . Ранее мы говорили о нагреве газа и показали, что поскольку молекулы газа движутся, а движущиеся тела становятся массивнее, то при нагревании газа и усилении движения молекул газ становится тяжелее. Но на самом деле такое рассуждение является совершенно общим; наше обсуждение свойств неупругого соударения тоже показывает, что добавочная масса появляется всегда, даже тогда, когда она не является кинетической энергией. Иными словами, если две частицы сближаются и при этом образуется потенциальная или другая форма энергии, если части составного тела замедляются потенциальным барьером, производя работу против внутренних сил, и т. д.,— во всех этих случаях масса тела по-прежнему равна полной привнесенной энергии. Итак, вы видите, что выведенное выше сохранение массы равнозначно сохранению энергии, поэтому в теории относительности нельзя говорить о неупругих соударениях, как это было в механике Ньютона. Согласно механике Ньютона, ничего страшного не произошло бы, если бы два тела, столкнувшись, образовали тело с массой 2 m 0, не отличающееся от того, какое получилось бы, если их медленно приложить друг к другу. Конечно, из закона сохранения энергии мы знаем, что внутри тела имеется добавочная кинетическая энергия, но по закону Ньютона на массу это никак не влияет. А теперь выясняется, что это невозможно: поскольку до столкновения у тел была кинетическая энергия, то составное тело окажется тяжелее ; значит, это будет уже другое тело. Если осторожно приложить два тела друг к другу, то возникает тело с массой 2 m 0; когда же вы их с силой столкнете, то появится тело с большей массой. А если масса отличается, то мы можем это заметить . Итак, сохранение импульса в теории относительности с необходимостью сопровождается сохранением энергии.
Читать дальше

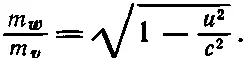 (16.9).
(16.9).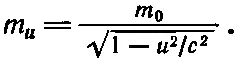 (16.10)
(16.10)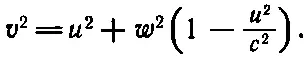
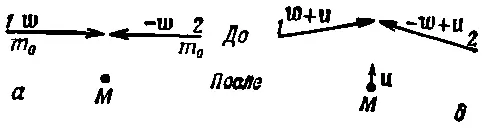
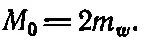 (16.11)
(16.11)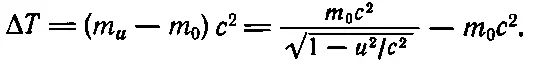 (16.12)
(16.12)




