На чем еще скажется релятивистский рост массы? Рассмотрим движение молекул газа в баллоне. Если газ нагреть, скорость молекул возрастет, а вместе с нею и их масса. Газ станет тяжелее. Насколько?
Разлагая m 0/√(1- v 2/ c 2)= m 0(1- v 2/с 2) -1/2в ряд по формуле бинома Ньютона, можно найти приближенно рост массы при малых скоростях. Получается
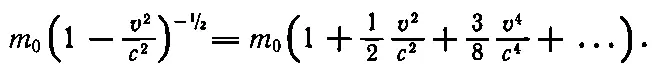
Из формулы ясно, что при малых v ряд быстро сходится и первых двух-трех членов здесь вполне достаточно. Значит, можно написать
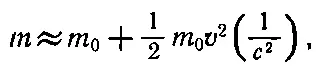 (15.11)
(15.11)
где второй член и выражает рост массы за счет повышения скорости. Когда растет температура, v 2растет в равной мере, значит, увеличение массы пропорционально повышению температуры. Но 1/ 2 m 0 v 2— это кинетическая энергия в старомодном, ньютоновом смысле этого слова. Значит, можно сказать, что прирост массы газа равен приросту кинетической энергии, деленной на с 2, т. е. Δm=Δ(к.э.)/с 2.
§ 9. Связь массы и энергии
Это наблюдение навело Эйнштейна на мысль, что массу тела можно выразить проще, чем по формуле (15.1), если сказать, что масса равна полному содержанию энергии в теле, деленному на с 2. Если (15.11) помножить на с 2, получается
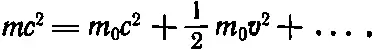 (15.12)
(15.12)
Здесь левая часть дает полную энергию тела, а в последнем члене справа мы узнаем обычную кинетическую энергию. Эйнштейн осмыслил первый член справа (очень большое постоянное число m 0 с 2) как часть полной энергии тела, а именно как его внутреннюю энергию, или «энергию покоя».
К каким следствиям мы придем, если вслед за Эйнштейном предположим, что энергия тела всегда равна mс 2? Тогда мы сможем вывести формулу (15.1) зависимости массы от скорости, ту самую, которую до сих пор мы принимали на веру. Пусть тело сперва покоится, обладая энергией m 0 с 2. Затем мы прикладываем к телу силу, которая сдвигает его с места и поставляет ему кинетическую энергию; раз энергия примется возрастать, то начнет расти и масса (это все заложено в первоначальном предположении). Пока сила действует, энергия и масса продолжают расти. Мы уже видели (см. гл. 13), что быстрота роста энергии со временем равна произведению силы на скорость
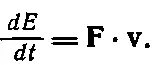 (15.13)
(15.13)
Кроме того, F= d ( m v)/ dt [см. гл. 9, уравнение (9.1)]. Связав все это с определением Е и подставив в (15.13), получим
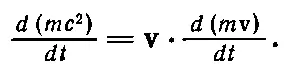 (15.14)
(15.14)
Мы хотим решить это уравнение относительно m. Для этого помножим обе части на 2m. Уравнение обратится в
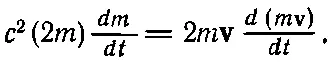 (15.15)
(15.15)
Теперь нам нужно избавиться от производных, т. е. проинтегрировать обе части равенства. В величине (2m) dm / dt можно узнать производную по времени от m 2, а в (2m v)· d (m v)/ dt — производную по времени от (mv) 2. Значит, (15.15) совпадает с
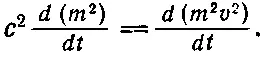 (15.16)
(15.16)
Когда производные двух величин равны, то сами величины могут отличаться не больше чем на константу С . Это позволяет написать
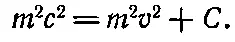 (15.17)
(15.17)
Определим теперь константу С явно. Так как уравнение (15.17) должно выполняться при любых скоростях, то можно взять v=0 и обозначить в этом случае массу через m 0. Подстановка этих чисел в (15.17) дает
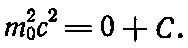
Это значение С теперь можно подставить в уравнение (15.17). Оно принимает вид
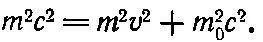 (15.18)
(15.18)
Читать дальше

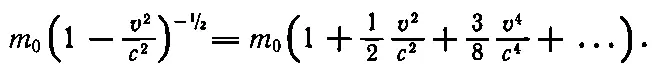
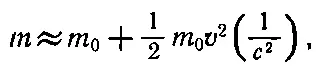 (15.11)
(15.11)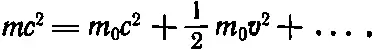 (15.12)
(15.12)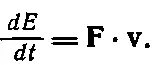 (15.13)
(15.13)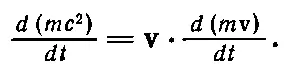 (15.14)
(15.14)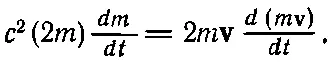 (15.15)
(15.15)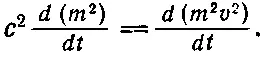 (15.16)
(15.16)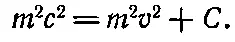 (15.17)
(15.17)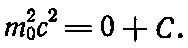
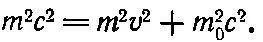 (15.18)
(15.18)




