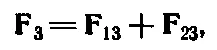
то работа равна
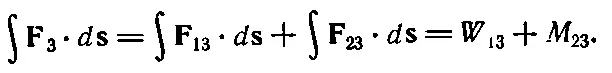
Стало быть, вся работа равна сумме работ, произведенных против силы 1 и против силы 2, как если бы они действовали независимо. Продолжая рассуждать таким образом, мы увидим, что полная работа, которую необходимо выполнить, чтобы собрать данную конфигурацию тел, в точности равна значению (13.14) для потенциальной энергии. Именно из-за того, что тяготение подчиняется принципу наложения сил, можно потенциальную энергию представить в виде суммы по всем парам частиц.
§ 4. Поле тяготения больших тел
Теперь рассчитаем поля, встречающиеся во многих физических задачах, когда речь идет о распределении масс . Мы пока не рассматривали распределения масс, а занимались только отдельными частицами. Но интересно рассчитать и поля, образуемые более чем одной частицей. Для начала найдем силу притяжения со стороны плоского пласта вещества бесконечной протяженности. Сила притяжения единичной массы в данной точке Р (фиг. 13.5), конечно, направлена к плоскости.
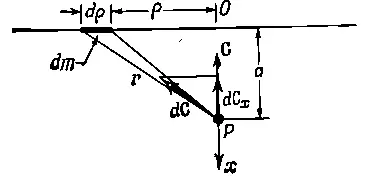
Фиг. 13.5. Сила притяжения материальной точки материальной плоскостью.
Расстояние от точки до плоскости есть a , а масса единицы площади этой плоскости есть μ. Пусть μ будет постоянной: слой однороден. Какой же величины поле d Cсоздается массой dm , удаленной от О не ближе, чем на p , и не дальше, чем на p+dp (О — это точка плоскости, ближайшая к Р)? Ответ: d C= G ( dm r/ r 3). Но оно, это поле, направлено вдоль r , а мы понимаем, что из трех составляющих Спосле сложения всех d Cдолжна остаться лишь x -составляющая. Она равна
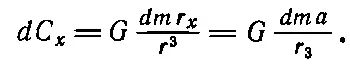
Все массы dm , которые находятся на одном и том же расстоянии r от Р , дадут одно и то же значение dC x , так что за dm можно сразу принять массу всего кольца между p и p + dp , т. е. dm =μ2π pdp (2π pdp — это площадь кольца радиусом p и шириной dp при dp ≪ p ). Итак,
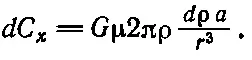
Но pdp=rdr из-за того, что r 2=p 2+a 2. Поэтому
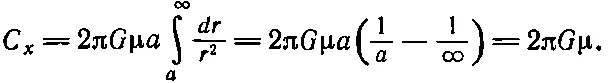 (13.17)
(13.17)
Стало быть, сила не зависит от расстояния а! Почему? Не ошиблись ли мы? Казалось бы, чем дальше от плоскости, тем сила слабее. Но нет! Если точка находится вплотную к плоскости, то большая часть вещества притягивает ее под неудачными углами, а если вдалеке, то у большей части вещества притяжение направлено прямее к плоскости. На любом расстоянии самая «влиятельная» часть плоскости лежит в некотором конусе. С удалением сила ослабляется обратно пропорционально квадрату расстояния, но в том же конусе под тем же углом оказывается больше вещества , а рост количества вещества тоже пропорционален квадрату расстояния! Этот анализ может быть сделан более строгим, если заметить, что дифференциал вклада любого данного конуса не зависит от расстояния в результате противоположных изменений напряженности поля данной массы и количества самой этой массы (с ростом расстояния). Впрочем, на самом деле сила не постоянна, ибо на другой стороне плоскости она меняет знак.
Мы решили, кстати, и задачу по электричеству: мы доказали, что у заряженной пластины, каждая единица площади которой несет заряд σ, электрическое поле равно σ/2ε 0и направлено от пластины , если она заряжена положительно, и к ней , если она заряжена отрицательно. Чтобы доказать это, надо просто вспомнить, что в законе тяготения G играет ту же роль, что 1/4πε 0в электричестве.
А теперь пусть имеются две пластины, одна с положительным зарядом +σ, а другая с отрицательным -σ (на единицу площади), и пусть промежуток между ними равен D . Каково поле этих пластин? Снаружи пластин поле равно нулю. Отчего? Оттого, что одна из них отталкивает, а другая притягивает и у обеих сила не зависит от расстояния ; значит, силы всюду уничтожаются! А вот поле между пластинами вдвое больше, чем поле одной пластины, направлено оно от положительной пластины к отрицательной и равно Е =σ/ε 0.
Читать дальше


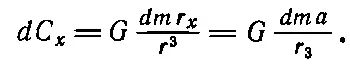
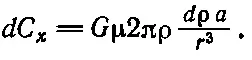
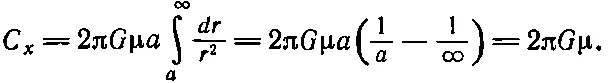 (13.17)
(13.17)




