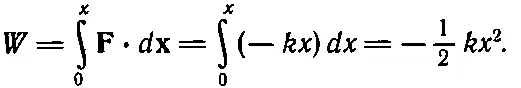
Значит, у массы, подвешенной на пружине, сумма кинетической энергии ее колебаний и 1/ 2 kx 2постоянна. Посмотрим, как это происходит. Оттянем массу вниз; она неподвижна и скорость ее равна нулю, но х не равно нулю, теперь величина х максимальна, так что имеется и некоторый запас энергии (потенциальной). Отпустим теперь массу: начнется какой-то процесс (в детали мы не вникаем), но в любое мгновение кинетическая плюс потенциальная энергии будут постоянны. Например, когда масса проходит через точку первоначального равновесия, то х =0, но тогда значение v 2наибольшее, и чем больше величина x 2, тем меньше v 2и т. д. Значит, во время колебаний соблюдается равновесие между величинами x 2и r 2. Мы получили, таким образом, новое правило: потенциальная энергия пружины равна 1/ 2 kx 2, если сила равна - kx .
Перейдем теперь к более общему случаю и рассмотрим, что произойдет, если тел много. Предположим, что имеется несколько тел; пронумеруем их: i =1, 2, 3, ... и пусть все они притягивают друг друга. Что тогда произойдет? Можно доказать, что если сложить кинетические энергии всех тел и добавить сюда сумму (по всем парам частиц) их взаимных потенциальных энергий тяготения — GMm / r ij , то все вместе даст постоянную:
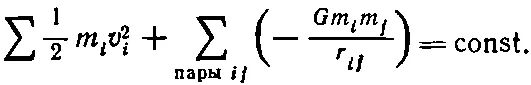 (13.14)
(13.14)
Как же это доказать? Мы продифференцируем обе стороны по времени и докажем, что получится нуль. При дифференцировании 1/ 2 m i v i 2мы получим производные скорости — силы [как в (13.5)], а потом эти силы заменим их величиной, известной нам из закона тяготения, и увидим в конце концов, что останется как раз производная по времени от
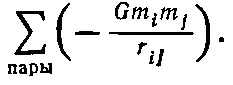
Начинаем доказательство. Производная кинетической энергии по времени есть
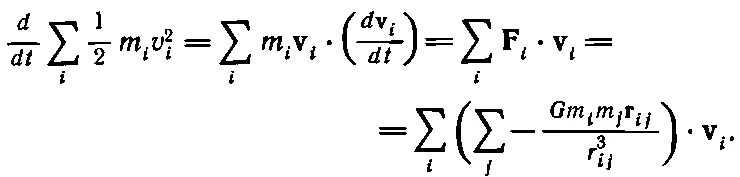 (13.15)
(13.15)
Производная по времени от потенциальной энергии есть
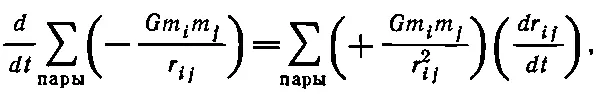
но
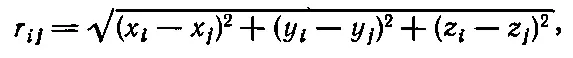
так что
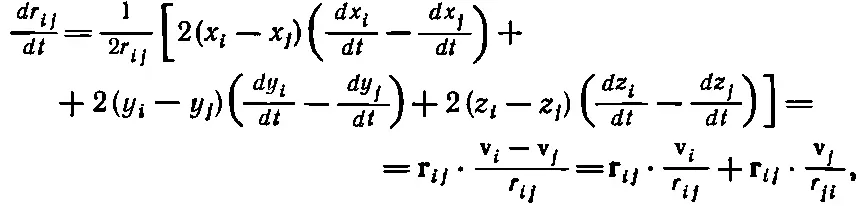
потому что r ij=- r ji, хотя r ij = r ji . Итак,
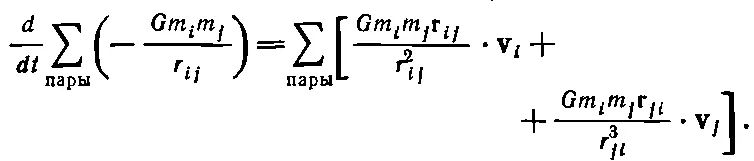 (13.16)
(13.16)
Теперь внимательно посмотрим, что значит ∑ i {∑ j } и ∑ парыВ (13.15) ∑ i {∑ j } означает, что i принимает по порядку все значения i=1, 2, 3,..., и для каждого i индекс j принимает все значения, кроме i . Если, например, i =3, то j принимает значения 1, 2, 4, ....
С другой стороны, в (13.16) ∑ парыозначает, что каждая пара i и j встречается лишь однажды. Скажем, частицы 1 и 3 дают только один член в сумме. Чтобы отметить это, можно договориться, что i принимает значения 1, 2, 3, ..., а j для каждого i — только значения, большие чем i Если, скажем, i =3, то j равно 4, 5, 6, .... Но вспомним, что каждая пара i,j дает два слагаемых в сумме, одно с v i, а другое с v j , и что оба эти члена выглядят так же, как член в уравнении (13.14) [но только в последнем в сумму входят все значения i и j (кроме i = j )]. В уравнениях (13.16) и (13.15) член за членом совпадут по величине. Знаки их, однако, будут противоположны, так что производная по времени от суммы потенциальной и кинетической энергий действительно равна нулю. Итак, мы видим, что и в системе многих тел кинетическая энергия составляется из суммы энергий отдельных тел и что потенциальная энергия тоже состоит из взаимных потенциальных энергий пар частиц. Почему она складывается из энергий пар? Это можно уяснить себе следующим образом: положим, мы хотим найти всю работу, которую нужно совершить, чтобы развести тела на определенные расстояния друг от друга. Можно это сделать не за один раз, а постепенно, доставляя их одно за другим из бесконечности, где на них никакие силы не влияли. Сперва мы приведем тело 1, на что работы не потребуется, потому что, пока нет других тел, силы отсутствуют. Доставка тела 2 потребует работы W 12=- Gm 1 m 2/ r 12. И вот теперь самый существенный момент: мы доставляем тело 3 в точку 3. В любой момент сила, действующая на 3, слагается из двух частей: из силы, действующей со стороны 1, и силы со стороны 2. Значит, и вся произведенная работа равна сумме работ каждой из сил , потому что раз F 3разбивается на сумму сил
Читать дальше

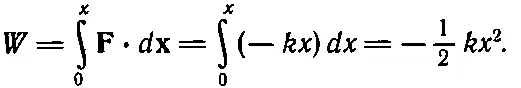
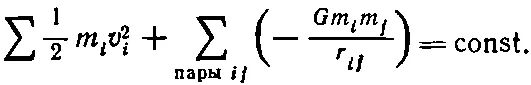 (13.14)
(13.14)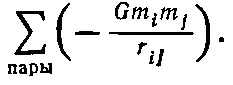
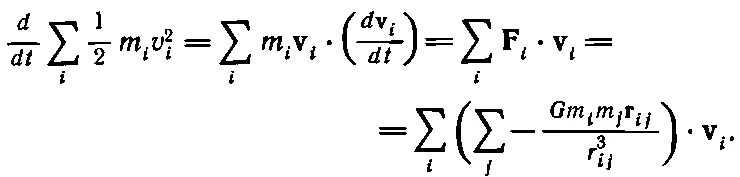 (13.15)
(13.15)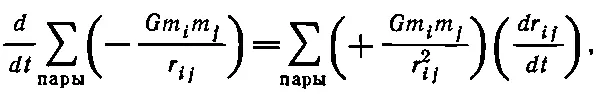
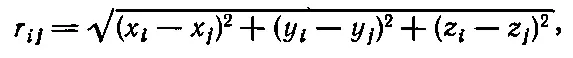
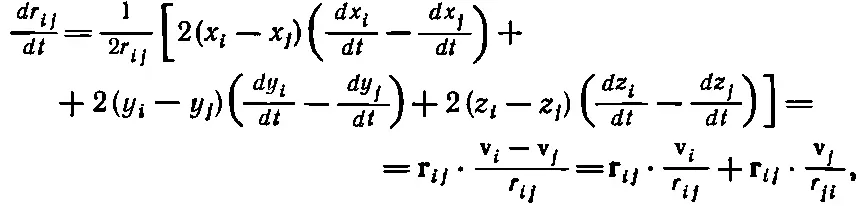
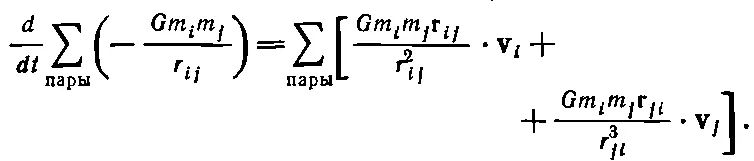 (13.16)
(13.16)




