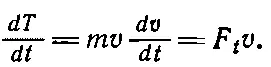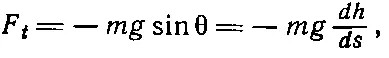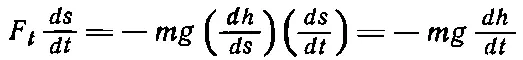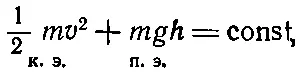
или
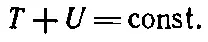 (13.1)
(13.1)
Мы хотим показать, что это утверждение правильно. Что значит доказать его правильность? Второй закон Ньютона говорит, как движется тело, как со временем изменяется его скорость (а именно, что в падении она растет пропорционально времени, а высота падения меняется как квадрат времени). Если поэтому отмерять высоту от нулевой точки (где тело покоилось), то не будет ничего странного в том, что она окажется равной квадрату скорости, умноженному на какие-то постоянные. Однако все же рассмотрим это повнимательней.
Попробуем вычислить прямо из второго закона Ньютона, как обязана меняться кинетическая энергия; мы продифференцируем кинетическую энергию по времени и потом применим закон Ньютона. Дифференцируя 1/ 2 mv 2по времени, получаем
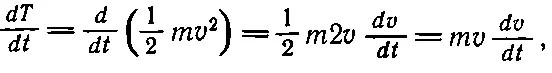 (13.2)
(13.2)
потому что m считается постоянной. Но по второму закону Ньютона m ( dv / dt )= F , так что
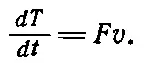 (13.3)
(13.3)
В общем случае получается F· v, но для нашего одномерного случая лучше оставить просто произведение силы на скорость.
Сила в нашем простом примере постоянна, равна — mg и направлена вниз (знак минус именно это и показывает), а скорость есть степень изменения положения по вертикали (высоты h ) со временем. Поэтому степень изменения кинетической энергии равна — mg ( dh / dt ). Взгляните: что за чудо! Перед нами снова чья-то скорость изменения — скорость изменения со временем величины mgh ! Поэтому выходит, что с течением времени изменения в кинетической энергии и в величине mgh остаются равными и противоположными, так что их сумма остается неизменной. Что и требовалось доказать.
Мы только что показали, пользуясь Вторым законом Ньютона, что для постоянных сил энергия сохраняется, если только прибавлять потенциальную энергию mgh к кинетической 1/ 2 mv 2. Исследуем этот вопрос дальше; посмотрим, можно ли его обобщить, можно ли еще продвинуться в его понимании. Действует ли этот закон только для свободно падающих тел или является более общим? Из того, что мы знаем о сохранении энергии, можно ожидать, что он будет верен для тела, движущегося из одной точки в другую по кривой без трения и под действием одной лишь тяжести (фиг. 13.1).
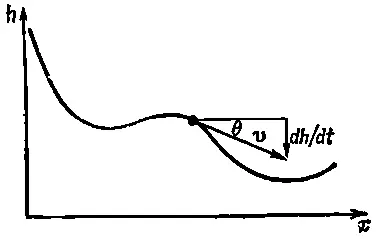
Фиг. 13.1. Тело, движущееся под действием тяжести по кривой без трения.
Когда тело, начав двигаться с высоты Н , достигает высоты h , то опять должна быть верной та же формула, хотя бы скорость уже не была направлена по вертикали. Нам надо понять, почему она все еще правильна. Проведем тот же анализ; отыщем скорость изменения кинетической энергии во времени. Опять будет получаться mv ( dv / dt ) — скорость изменения величины импульса, т. е. сила в направлении движения — касательная сила F t . Итак,
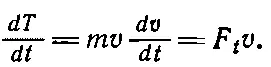
Скорость — это скорость изменения расстояния вдоль кривой ds / dt , а касательная сила F t теперь оказывается меньше mg в отношении, равном отношению расстояния ds вдоль пути к вертикальному расстоянию dh . Иными словами,
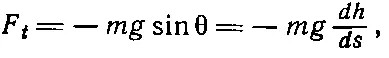
так что
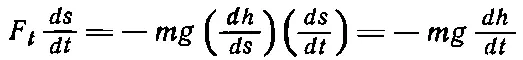
( ds выпадает). И опять, как прежде, мы получили величину — mg ( dh / dt ), равную скорости изменения mgh .
Чтобы точно уяснить себе, как вообще соблюдается сохранение энергии в механике, рассмотрим сейчас некоторые полезные понятия.
Во-первых, рассмотрим скорость изменения кинетической энергии в общем трехмерном случае. Кинетическая энергия, когда движение имеет три измерения, равна
Читать дальше

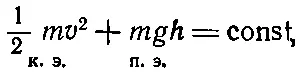
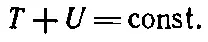 (13.1)
(13.1)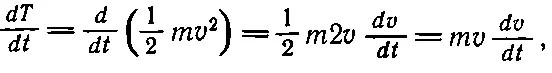 (13.2)
(13.2)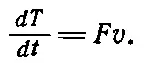 (13.3)
(13.3)