Лоуренс Краусс - Почему мы существуем? Величайшая из когда-либо рассказанных историй

Задним числом можно сказать, что мы, физики, могли бы догадаться (просто из соображений симметрии, без непосредственного рассмотрения эффекта Мейснера), что фотоны внутри сверхпроводника должны бы, в принципе, вести себя как массивные частицы. Конденсат куперовских пар состоит из электронов и потому обладает суммарным электрическим зарядом. Это нарушает калибровочную симметрию электромагнетизма, потому что на этом фоне любые положительные заряды, добавленные к веществу, будут вести себя иначе, чем добавленные отрицательные заряды. Так что теперь существует реальное различие между положительным и отрицательным. Но не забывайте, что отсутствие массы у фотонов – признак того, что электромагнитное поле является дальнодействующим, а дальнодействующая природа электромагнитного поля говорит о том, что локальные вариации в определении электрического заряда в одном месте не влияют на физические законы глобально, во всем объеме вещества. Но если калибровочная инвариантность пропала, то локальные изменения в определении электрического заряда будут иметь реальный физический эффект, и такого дальнодействующего поля, которое могло бы гасить эти изменения, существовать не может. Один из способов избавиться от дальнодействующего поля состоит в том, чтобы сделать фотон массивным.

А теперь вопрос на 64 000 долларов: а не может ли что-то подобное происходить в мире, где мы обретаемся? Может ли причиной наличия масс у тяжелых фотоноподобных частиц служить то, что на самом деле мы живем в чем-то похожем на космический сверхпроводник? Именно этот жгучий вопрос поднял Андерсон, по крайней мере в части аналогии с настоящими сверхпроводниками.

Прежде чем ответить на этот вопрос, нам необходимо разобраться в некотором техническом волшебстве, позволяющем наделить массой фотон в сверхпроводнике.

Вспомним, что в электромагнитной волне электрическое (E) и магнитное (B) поля колеблются туда-сюда в направлениях, перпендикулярных направлению движения волны, как показано на рисунке.

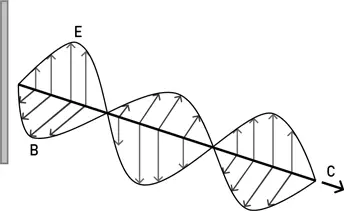
Поскольку перпендикулярных направлений два, электромагнитную волну можно изобразить двумя способами. Волна может выглядеть так, как показано на рисунке, а можно поменять поля E и B местами. Это результат того, что электромагнитные волны имеют две степени свободы, которые называют двумя разными поляризациями.

Это объясняется калибровочной инвариантностью электромагнетизма или, что то же самое, отсутствием у фотона массы. Однако если бы у фотонов была масса, то результатом стало бы не только нарушение калибровочной инвариантности, но и возникновение третьего варианта. Электрическое и магнитное поля могли бы колебаться вдоль направления движения, вместо того чтобы придерживаться только перпендикулярных к нему направлений. (Поскольку фотоны уже не двигались бы со скоростью света, стали бы возможны колебания вдоль направления движения частиц.)

Но это означает, что соответствующие массивные фотоны должны иметь не две, а три степени свободы. Как же могут фотоны в сверхпроводниках обрести эту лишнюю степень свободы?

Андерсон исследовал этот вопрос в сверхпроводниках, и его решение тесно связано с фактом, о котором я уже говорил. Если бы в сверхпроводнике не было электромагнитных взаимодействий, в конденсате куперовских пар можно было бы производить небольшие пространственные изменения с энергозатратами сколь угодно малой величины, потому что куперовские пары не взаимодействовали бы друг с другом. Однако, если принять во внимание электромагнетизм, эти низкоэнергетические моды (которые уничтожили бы сверхпроводимость) исчезают, и как раз потому, что заряды в конденсате взаимодействуют с электромагнитным полем. Это взаимодействие заставляет фотоны в сверхпроводнике вести себя так, как если бы они обладали массой. Новый режим поляризации массивных фотонов в сверхпроводнике возникает, когда конденсат колеблется в ответ на проходящую электромагнитную волну.

На языке физики элементарных частиц безмассовые моды Намбу – Голдстоуна, соответствующие корпускулярному варианту исчезающе малых в ином случае энергетических колебаний в конденсате, «съедаются» электромагнитным полем, что придает фотонам массу и новую степень свободы и делает электромагнитное взаимодействие в сверхпроводнике близкодействующим.