Георгий Гамов - Мистер Томпкинс внутри самого себя

сто назад шведским математиком Мёбиусом.

— А что такое лист Мёбиуса и как он мог привести к разрыву помолвки между двумя любящими друг друга молодыми людьми? — спросил вконец озадаченный отец.

— Дай мне, пожалуйста, листок бумаги, карандаш, ножницы и капельку клея, — попросил Уилфред.

Пораженный странной просьбой, мистер Томпкинс принес все, о чем просил сын. Взяв листок бумаги, Уилфред отрезал от него полоску шириной около 6 сантиметров и, повернув один из концов на полоборота, склеил концы. Получилось кольцо.

— Это и есть лист Мёбиуса, - пояснил он. — В отличие от других колец, имеющих две стороны, внутреннюю и внешнюю, у листа Мебиуса есть только одна поверхность. Его невозможно выкрасить в белый цвет изнутри и в черный снаружи или посеребрить изнутри и позолотить снаружи, поскольку у него только одна сторона. И если начать красить лист Мёбиуса с какой-нибудь точки, безразлично где она будет расположена, на «внутренней» или на «внешней» стороне, то, вернувшись в исходную точку, ты обнаружишь, что выкрашено в один и тот же цвет все кольцо целиком.

— Я еще могу понять, — упрямо возразил мистер Томпкинс, — что обручальные кольца играют важную роль в браке, но, признаться, не постигаю, каким образом кольцо, которое ты называешь листом Мебиуса, могло разорвать твою помолвку с Верой и довести тебя до того состояния, в котором ты сейчас находишься.

— Как ты уже знаешь, отец Веры возражал против нашего брака потому, что я не мог быть ничем полезным в том деле, которым он занимался, — обувной промышленности. Однажды бессонной ночью мне пришло в голову, что изготовление обуви на правую и левую ногу требует двух типов станков. А нельзя ли, подумал я, изготавливать всю обувь, скажем, на левую ногу, а затем половину обуви с помощью какого-нибудь топологического трюка превращать в обувь на правую ногу? Если бы такое было возможно, то себестоимость продукции можно было бы уменьшить.

— А какое отношение к этому имеет лист Мёбиуса? — с интересом спросил мистер Томпкинс.

— Дело в том, — пояснил Уилфред, — что при обходе листа Мёбиуса объекты, как говорят ныне физики, меняют «четность». Я продемонстрирую тебе это на том листе Мёбиуса, который только что склеил для тебя.

С этими словами Уилфред достал свою авторучку и нарисовал на листе Мёбиуса матадора с красным плащом в одной руке и острой шпагой в другой, стоящим лицом к быку.

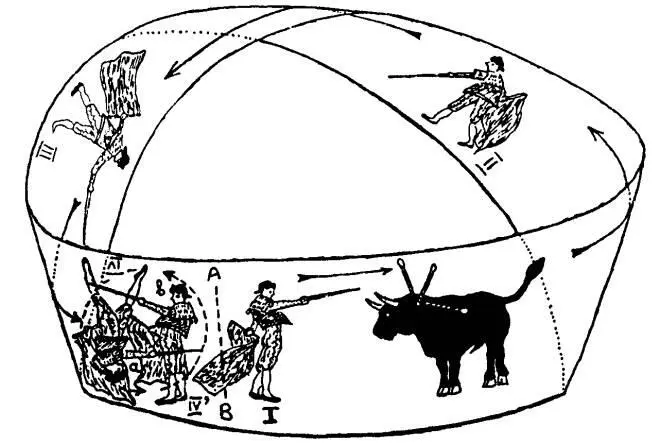
— Как тебе, должно быть, известно, — начал Уилфред, — поверхность по Евклиду не имеет толщины, поэтому то, что нарисовано с одной стороны поверхности, прекрасно видно и с другой. Может быть, в этой случае вместо обычного листа бумаги лучше взять прозрачный целлофан. На моем рисунке матадор находится по отношению к быку в правильном положении и имеет хороший шанс нанести быку решающий удар своей шпагой. Но представь себе что матадор обходит быка, обегает лист Мёбиуса и возвращается на арену. Вернувшись в исходную точку, он снова окажется лицом к быку, но при этом будет стоять на голове. Разумеется, сражаться с быком в таком положении, мягко говоря, не очень сподручно. Поскольку матадор не может выйти из двумерной поверхности, в которой он находится, ему не остается ничего другого, кроме как повернуться на 180 градусов в поверхности.

Но, встав с головы на ноги, матадор окажется стоящим спиной к быку. В таком положении сражаться с быком тоже не очень сподручно.

Таким образом, матадору настоятельно не рекомендуется обегать лист Мёбиуса!

Мистер Томпкинс не на шутку забеспокоился: его мальчик, который прежде был таким разумным и так ясно мыслил, теперь нес несусветную чушь.

— Какое отношение имеет все это к разрыву твоей помолвки с Верой? — удивился мистер Томпкинс.

— Самое непосредственное, — печально ответил Уилфред. — Как ты, должно быть, заметил, матадор, совершив обход листа Мёбиуса, превратился в свое зеркальное отражение. В ту бессонную ночь мне пришло в голову, что в трехмерном пространстве также может существовать трехмерный аналог листа Мёбиуса, столь хорошо известного в теории двумерных поверхностей. Согласно знаменитому немецкому математику Бернгарду Риману, жившему около ста лет назад, трехмерное пространство может быть искривлено, как и обычная двумерная поверхность. Риманова геометрия лежит в основе общей теории относительности Эйнштейна. А поскольку в геометрии двумерных поверхностей существует лист Мёбиуса, модель которого я склеил для тебя из бумаги, то почему бы в трехмерном пространстве не существовать его трехмерному аналогу — этакой воронке Мёбиуса? При обходе воронки различные тела превращались бы из своих правосторонних модификаций в левосторонние. И тут я вспомнил, что прочитал где-то об одной экспедиции биологов в верховья Амазонки. Участники экспедиции обнаружили две разновидности улиток с зеркально симметричными раковинами. А что если в тех местах, подумал я, ось воронки Мёбиуса пересекается с поверхностью Земли? Если моя догадка верна, то обе разновидности улиток первоначально ничем не отличались, но впоследствии часть улиток, мигрируя, совершила обход вокруг оси воронки Мёбиуса и превратилась в свое зеркальное отражение.