Георгий Гамов - Мистер Томпкинс внутри самого себя

— А что такое топология? — полюбопытствовал мистер Томпкинс.

Природная любознательность мистера Томпкинса явно брала верх над беспокойством по поводу неурядиц сына.

— Топологией называется раздел математики, — начал Уилфред, несколько задетый тем, что его отец больше интересуется абстрактными математическими проблемами, чем сердечными делами единственного сына. — Занимается топология изучением таких свойств тел в пространствах любого числа измерений, которые инвариантны, или неизменны относительно любых деформаций, производимых без разрезания тел или склеивания каких-нибудь его точек.

— Сын мой, не мог бы ты говорить вразумительнее? — спросил мистер Томпкинс. — Последнее время я интересовался многими проблемами естественных наук, а также математики, по поводу которой Бертран Рассел в одной из своих книг заметил, что математика — не наука, а искусство. Не мог бы ты привести несколько примеров топологических задач?

— Хорошо, — согласился Уилфред. Он и сам понял, что заговорил на языке, не очень понятном для неспециалиста. — Предположим, что ты сравниваешь два мяча — один для европейского, а другой — для американского футбола. Европейский мяч имеет идеальную сферическую форму. Предполагается, что по нему бьют ногой. Американский мяч имеет форму вытянутого эллипсоида. Предполагается, что игроки держат его в руках и бросают рукой за исключением тех случаев, когда правила разрешают бить по нему ногой. Деформируя мяч, т.е. растягивая или сжимая его кожаную поверхность, ты можешь превратить эллипсоидальный американский футбольный мяч в идеально сферический европейский. В топологии такие деформации, т. е. всевозможные растяжения или сжатия, считаются допустимыми. Не разрешается резать мяч ножом. Возьмем другой пример: велосипедную шину и бублик.

У шины в середине огромная дыра, у бублика дырка намного меньше.

Но опять-таки с помощью растяжений и сжатий ты можешь превратить велосипедную шину в точное подобие бублика или, наоборот, бублик — в подобие шины. Но как бы ни хотел, тебе не удастся, растягивая и сжимая, превратить футбольный мяч в велосипедную шину или бублик.

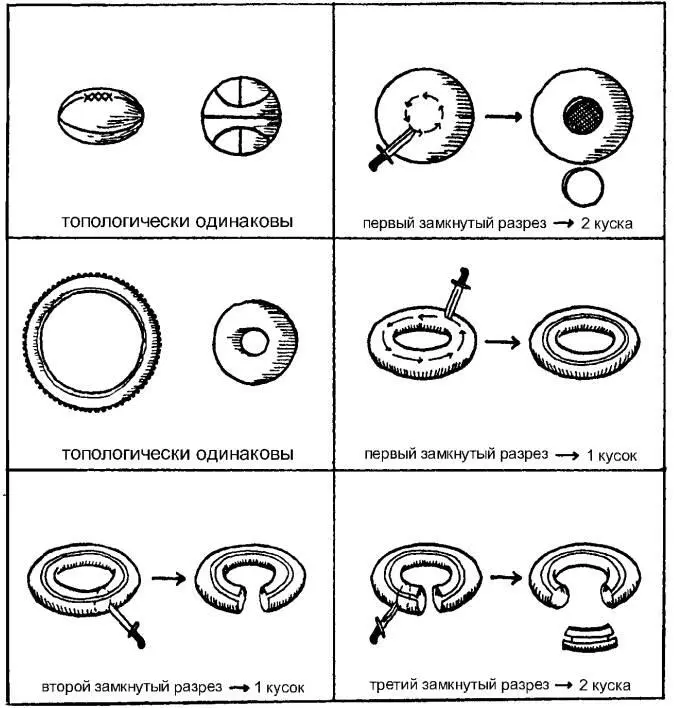
Между футбольным мячом и велосипедной шиной существует еще одно важное различие. Если воткнуть нож в поверхность футбольного мяча, американского или европейского, и провести разрез вдоль любой замкнутой не самопересекающейся линии, то мяч распадется на две отдельные части. Но если взять велосипедную шину, то разделить ее на две части одним замкнутым разрезом уже не удастся. Более того, шина может не распасться на две части и после того, как ты проведешь второй разрез. И только после третьего разреза шина неизбежно распадется на две части.

Простейшее из того, о чем нам говорит топология, среди некоторых других вещей состоит в предсказании того, на сколько частей распадется данная поверхность, если провести данное число разрезов.

— Детские игрушки! — возмущенно фыркнул мистер Томпкинс. — Почему так важно знать, на сколько частей распадется поверхность?

— Ты же сам процитировал Рассела, — возразил Уилфред, — утверждавшего, что математика — не наука, а искусство. Не мог бы ты сказать мне, почему так важно искусство?

— Проще простого! — воскликнул мистер Томпкинс. — Искусство доставляет удовольствие людям, которые любуются картинами, читают стихи или слушают музыку.

— Ты прав! — горько заметил Уилфред — но получает или не получает человек удовольствие, зависит от того, как он воспринимает красоту искусства. Я знаю нескольких людей, например, Вериного отца, который не даст и гроша за искусство, будь то живопись, поэзия или музыка!

И, исчерпав доводы, Уилфред обессиленно откинулся на спинку кресла.

Отцовский инстинкт все же взял свое, и мистер Томпкинс почувствовал, что своими вопросами увел разговор в сторону.

— Прости, пожалуйста, мой мальчик, — сказал он, — но расскажи мне лучше о Вере. Как прошла ваша последняя встреча перед твоим возвращением домой?

— Я не видел ее с тех самых пор, как расстроилась наша помолвка.

— Ваша помолвка расстроилась! — воскликнул пораженный мистер Томпкинс. — Но почему?!

— Потому, — печально ответил Уилфред, — что я с головой ушел в математические проблемы и не подумал об их возможных биологических последствиях. Как ты знаешь, я занимался топологией, в частности, листом Мёбиуса, интереснейшим объектом, изобретенным лет