Julian Barbour - The End of Time - The Next Revolution in Physics

I am not claiming that the description of space-time given by Einstein or Minkowski is wrong. Far from it – they got it right, but they described the finished product, and the complete story must also include the construction of the product. This is best done directly for the space-time of general relativity, the topic of the next chapters. As preparation for them, I conclude this chapter with a summary of the most important points.

Minkowski space-time is not some amorphous bulk in which there is no simultaneity structure at all. We can ‘paint coordinate lines’ – and an associated simultaneity structure – on space-time in many different ways. But the whole content of the theory would be lost if we could not do it one way or the other. There is no doubt about it – simultaneity hyperplanes exist out there in space-time as distinguished features.

Moreover, to give any content to relativity, we must, almost paradoxically, assume a universality of three-dimensional things. The clocks we can find in one Lorentz frame must be identical to the clocks we can find in any other. This is a prerequisite of the relativity principle, for it says that the laws of physics are identical in any such frame. That would be impossible if a particular kind of clock could exist in one frame but not in another. We can go further. On any hyperplane in any Lorentz frame, the actual things in the world (electric and magnetic fields, charged particles, etc.) can have any one of a huge number of different arrangements. Each of them is just like the possible distributions of particles from which we constructed Platonia for Newtonian physics.

Exactly the same thing can be done in relativity. There is a Minkowskian Platonia, whose points are all possible distributions of fields and matter that one can find on any simultaneity hyperplane in Minkowski space. Whatever Lorentz frame we choose, the Minkowskian Platonia always comes out the same. If it were not, the relativity principle, with its insistence that the laws of nature are identical in all Lorentz frames, would be meaningless. To be identical, the laws must operate on identical things, which are precisely the distributions that define the points of Platonia. For all its four-dimensional integrity, space-time is built of three-dimensional bricks. The beautiful four-dimensional symmetries hide the vital role of the bricks.

It is just that space-time is not constructed from a unique set. The analogy with a pack of cards is again quite apt. Newtonian space-time is an ordinary pack; Minkowski space-time is a magical pack. Look at it one way, and cards run through the block with one inclination. Look at it another way, and different cards run with a different inclination. But whichever way you look, cards are there.

This chapter is about how Einstein progressed from special relativity, which does not incorporate gravity, to general relativity, which does. Einstein believed that he was simultaneously incorporating Mach’s principle as its deepest foundation, but later, as I said, he changed his mind and left this topic in a great muddle. My view is that, nevertheless, without being aware of it, Einstein did incorporate the principle. This has important implications for time. We start with a bit more about Minkowski’s discoveries, which is necessary if we are to understand the way Einstein set about things.

One of the most important concepts in physics and geometry is distance, which is measured with rods. Distances can be measured in a space of any number of dimensions. You can measure them along a line or curve, on a flat or curved surface, or in space. In Part 2 we saw how an abstract ‘distance’, the action, can be introduced in multidimensional configuration spaces like Platonia. Minkowski showed that a remarkable kind of four-dimensional distance exists in space-time. Its existence is a consequence of the experimental facts that underlie special relativity. These things are most easily explained if we assume that space has just one dimension, not three; space-time then has two dimensions. Such a space-time is shown in Figure 27. We must first of all learn about past, present, and future in space-time.

One of the distinguished coordinate systems that exists in space-time is shown in Figure 27, in which the x axis is for space and the t axis for time, which increases upward. This is the Lorentz frame of Alice in Figure 25. Her world line is the vertical t axis. The units of time and distance are chosen to make the speed of light unity. Light pulses that pass through event O at t = 0 in opposite directions in space travel in space-time along the two lines marked future light cone . Their continuations backward (the light’s motion before it reaches O) define the past light cone .

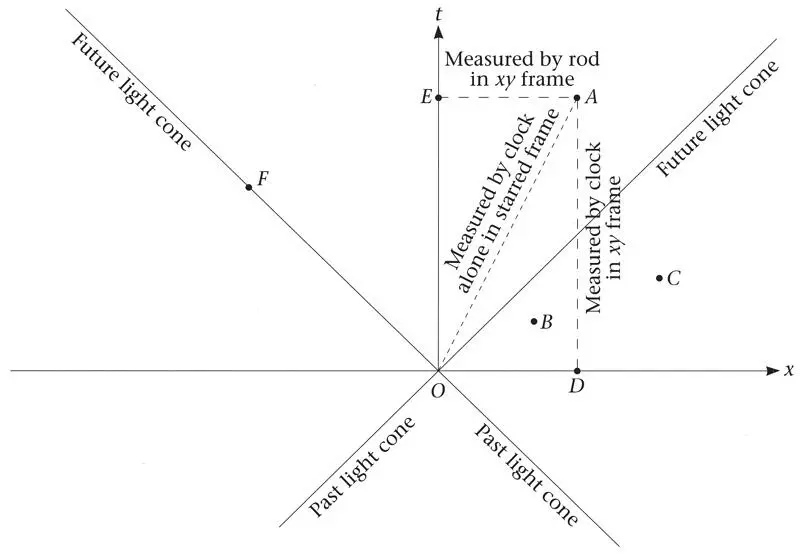
Figure 27.Past and future light cones and the division of space-time in time-like and space-like regions, as described in the text.

Each event has a light cone, but only O’s is shown. Relativity differs from Newtonian theory mainly through the light cone and its associated distinguished speed c , which is a limiting speed for all processes. Light plays a distinguished role in relativity simply because it has that speed. No material object can travel at or faster than it. If a material object passes through O, its world line must lie somewhere inside the light cone, for example OA in Figure 27.

The light cone divides space-time into qualitatively different regions. An event like A can be reached from O by a material object travelling slower than light. Two such events are time-like with respect to each other. For two such events there exists a Lorentz frame in which they have the same space coordinates but different time coordinates. For the points O and A this frame is shown in the upper right of Figure 28.

Next we consider events like B and C in Figure 27, outside the light cone of O . They are space-like with respect to O . No material body can reach them from O , since to do so it would have to travel faster than light. For two events that are mutually space-like there exists a Lorentz frame in which they have the same time coordinate but different space coordinates. For two space-like events, it is impossible to say which is the earlier in any absolute sense. In some Lorentz frames one will be earlier than the other (thus O is earlier than both B and C in Alice’s frame in Figure 27), but in others the temporal order will be reversed.

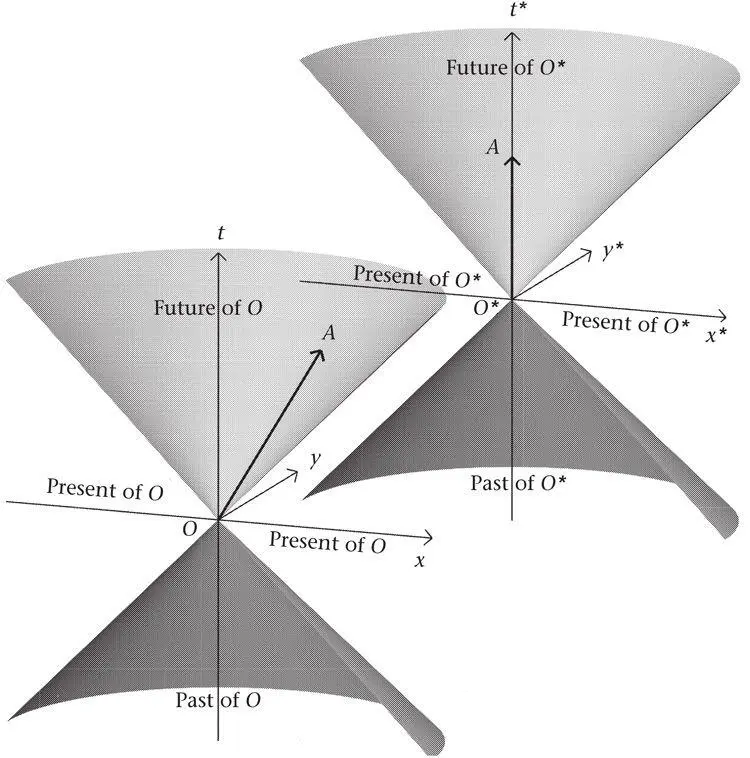
Figure 28.Past, present and future in a space-time with two dimensions of space. The object that moves along OA (bottom left) is at rest in the starred frame (top right). Its world line is O*A (O and O* are the same event).

Finally, two events that can be connected by a light ray have a light-like relationship. All points on the light cone of event 0, for example the point F , are light-like with respect to O .

These three basic relationships between events – being time-like, spacelike or light-like – are the same in all Lorentz frames. This is because the three types are determined by the light cones, which are real features in space-time, just as rivers are real features of a continent. In contrast, the coordinate axes are like lines ‘painted’ on space-time – they are no more real than the grid lines on a map. Moreover, in a change from one frame to another, the coordinate axes never cross the light cones. The time axis moves but stays within the light cone, while the space axes stay within the ‘present’ as defined above. This is illustrated in Figure 28 for space with two dimensions, which shows how the light cone gets its name. It also highlights the great difference between the Newtonian and Einsteinian worlds. In the former, past, present and future are defined throughout the universe, and the present is a single simultaneity hyperplane. In the latter, they are defined separately for each event in space-time, and the present is much larger.