Грегори Гбур - Загадка падающей кошки и фундаментальная физика

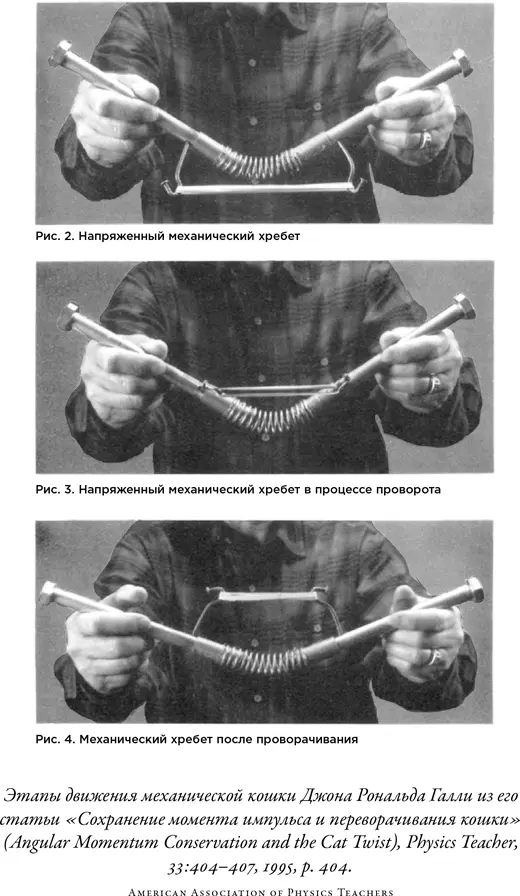
Галли построил несколько моделей кошки возрастающей сложности; действие простейшей из них показано на рисунке. Два цилиндра здесь работают как передняя и задняя половины кошки; пружина — как гибкий хребет. Резинка между двумя половинками тела действует как напряженная мышца; когда кошку выпускают из рук, напряжение резинки заставляет части тела «сложиться и крутиться», что приводит к перевороту на 180°.

Модель Галли в общем смысле можно отнести к категории биоробототехнического моделирования. Это устройство стало стандартным инструментом преподавателей физики, заинтересованных в том, чтобы объяснить задачу своим студентам. До недавнего времени доработанный вариант кошки Галли можно было приобрести онлайн, в комплекте с лапами, дополнительными секциями хребта и проволочной кошачьей мордой.

Создать надежную «кошачью» стратегию переворачивания в воздухе для робота более сложная задача. Поскольку кошка может падать под разными углами (в перевернутом состоянии, на боку, головой вниз и т. д.) и начинать падение с ненулевым или нулевым моментом импульса, ни один простой сценарий не позволит ей выправить положение в любой ситуации. Точное движение, при помощи которого перевернутая кошка сможет приземлиться в правильном положении, в другом случае, к примеру, перевернет кошку, падающую боком, на другой бок. Кошка — или робот — в падении должна принимать во внимание конкретные обстоятельства своего падения и соответствующим образом адаптировать стратегию, причем часто за долю секунды.

Сложность разработки робота, который способен был бы это делать, восходит опять же к задаче буриданова осла. Поскольку кошка может, в принципе, использовать множество разных методов переворачивания в правильное положение, то, если мы введем условие переворачивания за кратчайшее время, два метода могут показать одинаковую продолжительность, и тогда робот приземлится на спину только потому, что не смог сделать выбор. Как отметили исследователи: «Вопрос общей стратегии и контролируемого подхода к проблеме изменения ориентации сложной мультисегментной, мультисуставной системы без использования внешнего крутящего момента остается в значительной степени нерешенным. Сложность ответа на этот вопрос кроется в том факте, что в целом существует бесконечное число способов, при помощи которых мультисегментная мультисуставная система может произвольным образом изменить ориентацию в пространстве без применения внешнего эффективного крутящего момента» {18} .

Поэтому для создания робота, который не будет застревать между двумя в равной степени хорошими методами переворачивания, инженер должен ввести очень точное определение «хорошего» способа — определение, которое в любых возможных обстоятельствах позволит использовать лишь один возможный метод. Вот почему многие исследования переворачивания кошки сосредотачиваются исключительно на математическом решении этой задачи. В одной из ранних статей фотографии падающей кошки использовались для изучения роли вестибулярного аппарата в управлении движением падающей кошки {19} . Эта работа не имела отношения к робототехнике, но ее результаты послужат будущим исследователям ориентиром.

В 1998 г. Ара Арабян и Дерлян Цай из Университета Аризоны разработали алгоритмическую схему управления падающей кошкой, которая позволила бы ей успешно перевернуться. Эта схема, так же как ранее схема управления для шестиногих роботов, была децентрализованной; исполнительные механизмы, обеспечивающие работу суставов, должны были взаимодействовать между собой и обеспечивать обратную связь подобно проприоцептивным рефлексам. Авторы наложили на движение кошки несколько ограничений, как с самого начала предлагали сделать Кейн и Шер, чтобы ограничить трудность задачи, требующей решения, и вследствие этого избежать столкновения с буридановым ослом. Одно из созданных ими модельных решений задачи падающей кошки вполне сравнимо по качеству с компьютерной анимацией конца 1990-х гг. Как указывают авторы, результат их компьютерного моделирования очень близок к реальным фотографиям падающей кошки {20} .

Работа над математической стороной задачи о падающей кошке продолжается и в новом тысячелетии. В 2007 г. китайские исследователи использовали для поиска решений этой задачи метод, известный как неголономное планирование движения. В 2008 г. израильские исследователи предложили забавную модель «квадратной кошки», в которой кошка представляет собой четыре стержня равной длины, соединенные гибкими суставами, чтобы прояснить некоторые глубокие математические стороны задачи. В 2013 г. Ричард Кауфман из Массачусетского университета в Лоуэлле представил «электрическую кошку» — простую механическую модель животного, демонстрирующую маневр типа «сложись и крутись». Кауфман, в частности, пришел к выводу, что стратегии «сложись и крутись» более чем достаточно для реализации кошачьей способности и что метод «подожмись и поворачивайся» Марея играет в процессе в лучшем случае вторичную роль. В 2015 г. другая группа китайских исследователей применила для изучения динамики падающей кошки сложный математический аппарат — уравнение Удвадиа — Калабы {21} .