Грегори Гбур - Загадка падающей кошки и фундаментальная физика

Случилось так, что один исследователь в 1960-е гг. уже работал над решением аналогичных задач. Томас Кейн, профессор инженерной математики Стэнфордского университета, разработал к тому времени математический аппарат, позволявший анализировать движение сложных систем взаимосвязанных масс в условиях невесомости. Исследователи космоса тогда уже поняли пользу искусственной гравитации для астронавтов во время долгого пребывания в космосе, а одним из способов получения такой гравитации является вращение космического корабля или станции: в этом случае центробежная сила создаст в корабле или на станции направленное наружу ускорение, неотличимое от ускорения силы тяжести. В 1967 г. Кейн и его коллега Т. Р. Роуб исследовали стабильность спутника, состоящего из пары твердых объектов, соединенных каким-нибудь частично упругим мостиком, при условии вращения всей конструкции вокруг ее центра {22} . Традиционная модель падающей кошки, состоящая из пары цилиндров с гибким сочленением, очень напоминает эту конструкцию.

Кейн тоже занимался проблемой движения астронавта в условиях невесомости. Пользуясь своим новым математическим аппаратом, он показал, как можно вычислительными методами найти для астронавта оптимальные способы изменения ориентации {23} . Эта работа привлекла интерес NASA — агентство выдало исследователю грант в $60 000 на изучение подобных проблем. Примерно в это же время Кейн, очевидно, наткнулся на задачу о падающей кошке; не удовлетворившись прежними объяснениями, он попробовал применить к ним свои математические методы. Результатом его работы стала самая подробная и, вероятно, самая точная на сегодняшний день математическая модель падающей кошки.

Кейн, по большей части, согласился с объяснением переворота падающей кошки, которое дали Радемакер и тер Браак, а именно с моделью «сложись и крутись», но отметил в нем одно серьезное ограничение. В модели Радемакера и тер Браака кошка в процессе переворачивания сохраняет один и тот же угол сгиба между верхней и нижней половинами, из чего следует, что приземляться на лапы она будет с выгнутой в обратную сторону спиной — ровно наоборот по отношению к тому, что мы видим на самом деле. Кейн и его ученик М. П. Шер предположили вместо этого, что кошка начинает свое движение по Радемакеру и тер Брааку, но в процессе переворачивания постепенно выпрямляет спину (по существу, в сторону она смотрит уже практически с прямой спиной). Затем кошка сгибается в противоположную сторону, как бы начиная другое движение типа «сложись и крутись», и завершает падение приземлением на лапы с выгнутой горбом спиной и вытянутыми лапами. Короче говоря, в модели Кейна кошка производит движение Радемакера и тер Браака дважды с постепенным изменением изгиба спины.

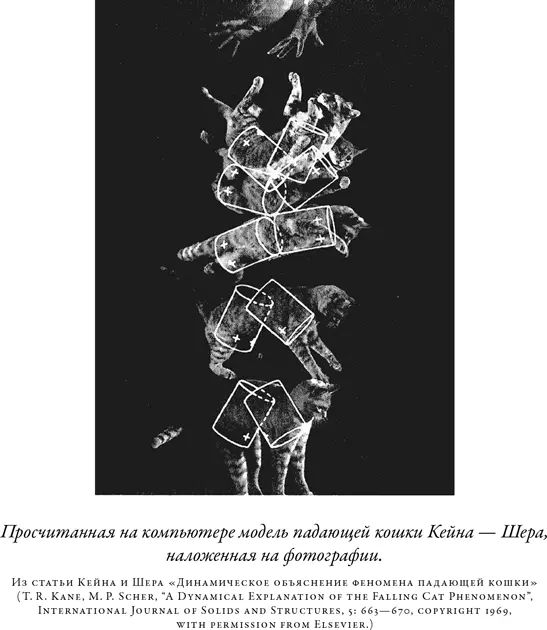
Модель Кейна и Шера проще визуализировать в виде трех последовательных отдельных движений. Представьте, что кошка, начиная падать, сгибается и проворачивается, пока не окажется мордой в сторону и согнутой вправо в поясе. Затем кошка сгибает свое тело в другую сторону, пока не окажется согнутой в поясе влево. С этого момента она может продолжить движение типа «сложись и крутись», пока не окажется согнутой вперед в поясе и смотрящей вниз.

В статье, опубликованной в 1969 г., Кейн и Шер наложили схематические изображения, полученные по расчетной модели, сверху на фотографии реальной падающей кошки {24} . Результаты получились убедительными. Подобно Радемакеру и тер Брааку, Кейн и Шер моделировали кошку в виде пары связанных цилиндров. На свою модель они наложили дополнительное ограничение: кошка не может проворачивать верхнюю и нижнюю секции тела относительно друг друга, как в модели «подожмись и поворачивайся» Марея.

Эта новая работа, связанная с кошками, в конечном итоге призвана была помочь астронавтам поворачиваться в условиях невесомости; любые методы, проработанные на кошках, необходимо было затем испытывать на людях. Как делали до него и Советы, Кейн использовал батут как дешевый способ создания кратковременной невесомости. Чтобы сконструировать новую методику поворота, Кейн для начала при помощи математических уравнений разработал способ оптимального переворачивания кошки. Затем он ввел эти движения в компьютер, что позволило ему визуально изобразить их понятным образом. Наконец, профессиональный акробат на батуте, надев скафандр, проверил, может ли человек, в принципе, эффективно воспроизвести эту технику.