Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Еще одна причина убедит вас атаковать острым концом яйца. В приведенных выше рассуждениях мы не учитывали наполняющую скорлупу жидкость, которая амортизируют столкновение. Так вот, со стороны тупого конца под скорлупой находится газовый мешок, более или менее крупный в зависимости от свежести яйца. Поэтому тупой конец оказывается более хрупким!

А что делать, если опытный противник и сам пытается атаковать вас острым концом? В этом случае постарайтесь поразить его биток сбоку, где кривизна ниже. Удачи!

3.1955 год. Нильс Бор и Вольфганг Паули изучают движение волчка Томсона

После боя на пасхальных яйцах сменим забаву и попробуем раскрутить яйцо в качестве волчка. Как известно, таким способом можно, не разбивая, отличить сырое яйцо от сваренного вкрутую. Последнее, содержимое которого стало твердым и неподвижным, может вращаться очень долго, в то время как сырое яйцо останавливается после всего лишь нескольких оборотов. Дело в том, что из-за вязкого трения его содержимого о скорлупу кинетическая энергия вращения рассеивается и постепенно переходит в тепло. Если остаются сомнения, то вот еще один тест: слегка коснувшись яйца пальцем, приостановите его вращение. При этом вы обнаружите, что, как только палец уберете, сырое яйцо спонтанно начнет вращаться. Это вращение уже порождается продолжающимся внутри яйца вращением жидкости.

Еще одно удивительное явление можно наблюдать, когда сваренное вкрутую яйцо сильно раскручивают (более десяти оборотов в секунду) на ровной, но не слишком гладкой поверхности, например вощеной ткани. После нескольких оборотов яйцо «встает на попа» и начинает вращаться на своем остром конце! Затем скорость его вращения постепенно падает, и яйцо возвращается в свое лежачее положение, при котором центр тяжести находится в низшем положении. Такое поведение сваренного вкрутую яйца подобно поведению китайского волчка (в англоязычных странах его называют «тип-топ» – tippe-top ), еще одного интересного чуда механики. Такой волчок имеет форму усеченной сферы, из которой выступает цилиндрическая ножка (илл. 4). Первоначально раскрученный вращением его ножки большим и указательным пальцами, волчок совершает несколько оборотов, стоя на сферической части, а затем вдруг переворачивается «на попа» и продолжает вращаться уже на ножке. Это необычное явление было объяснено физиком Уильямом Томсоном (1824–1907, впоследствии стал лордом Кельвином), поэтому эту игрушку иногда называют волчком Томсона. Важную роль тут играет трение об опору: сначала для раскрутки волчка из исходного положения, а затем для того, чтобы позволить ему выпрямиться на ножке. Волчки – это не только забавное шоу для детей и взрослых (илл. 3), но и неиссякаемый источник классических задач для студентов на экзаменах (см. врезку).

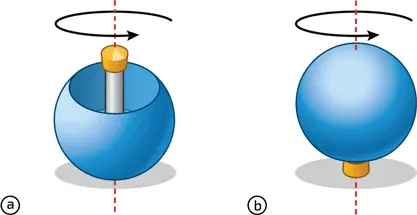
4. Удивительное свойство китайского волчка. Раскрученный с помощью хвостика в положении (a), через несколько оборотов волчок «становится на попа» и начинает вращаться в положении (b). При этом направление его вращения вокруг оси становится противоположным

Быстро вращающийся вокруг оси волчок не падает, если эта ось близка к вертикали. Как объяснить это явление?

Для простоты изучим движение волчка, имеющего форму поверхности вращения, а также предположим, что точка контакта C между волчком и опорой фиксирована (в случае китайского волчка или яйца это не так).

Характер движения волчка может быть определен на основании закона сохранения его момента импульса, или, как его еще называют, момента вращения. Этот закон для вращательного движения играет ту же роль, что и закон сохранения импульса для поступательного движения. Момент вращения L → – величина векторная. Этот вектор определяется распределением массы в объеме объекта, угловой скоростью его вращения, а также осью, относительно которой он вращается. Например, момент вращения крутящегося велосипедного колеса представляет собой вектор, перпендикулярный плоскости колеса, модуль которого пропорционален угловой скорости вращения. В частности, если волчок представляет собой набор материальных точек с массами m i , положение которых определяется относительно точки контакта векторами R i, а их линейные скорости суть v i , то его момент импульса L →представляет собой сумму векторных произведений m i R → i × V →(см. главу 4, «Смысл силы Кориолиса и векторное произведение»).