Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

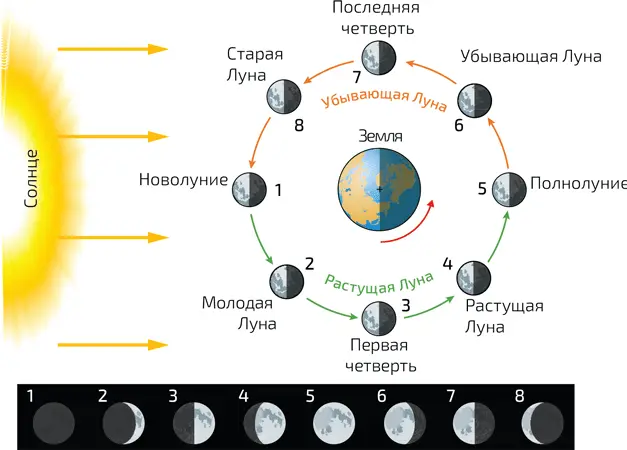
5. Фазы Луны. Для наблюдателя на Земле освещенная часть небесного тела зависит от его положения на орбите по отношению к Солнцу. От новолуния до следующего полнолуния проходит две недели

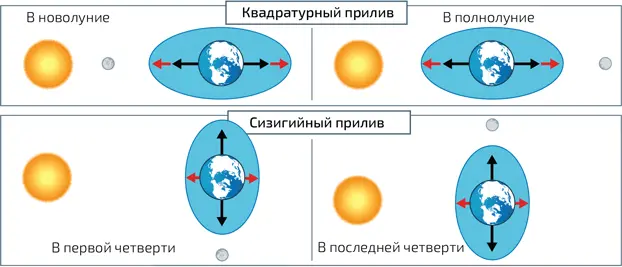
6. Во время полнолуния и новолуния силы Луны и Солнца накладываются друг на друга и приливы особенно сильны. Напротив, прилив смягчается во время первой и последней четверти

В точке, наиболее удаленной от Солнца (точка B), расстояние D до Солнца наибольшее, и его гравитационное притяжение оказывается слабее, в то время как центробежная сила оказывается большей, чем в точке А. Равнодействующая сила отбрасывает водные массивы от Солнца, и там тоже происходит прилив! Если бы Солнце было единственным небесным телом, вызывающим приливы, они происходили бы дважды в день: один в солнечный полдень, когда преобладает гравитационное притяжение, другой – в полночь, когда максимальна центробежная сила. В результате, если бы Земля была покрыта водой со всех сторон, она приняла бы форму удлиненного эллипсоида (как мы увидим, совсем немного удлиненного) или, как порой говорят, мяча для игры в регби (илл. 4). Удлинение вершин эллипсоида ограничено гравитационным притяжением водных масс самой Землей, которое, очевидно, сильнее, чем притяжение Луны и Солнца.

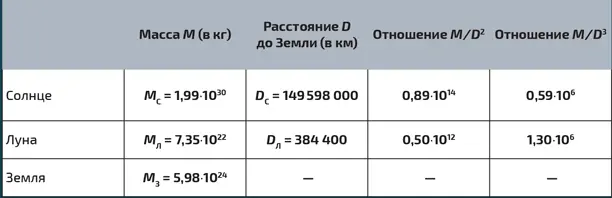
Данные для Земли, Луны и Солнца.Расчеты, приведенные в четвертом и пятом столбцах, позволяют сравнить удельные веса гравитационных сил, с которыми Солнце и Луна притягивают Землю, и действие этих небесных тел на приливы

Луна или Солнце – какое небесное тело сильнее влияет на приливы?

Чтобы упростить объяснение, ограничимся рассмотрением наиболее близкой к притягивающему небесному телу точки A (илл. 4) и наиболее удаленной от него точки B – таких, что в них обе силы F → 1(гравитационная) и F → 2(центробежная) лежат на прямой Земля – Солнце или Земля – Луна. В таком случае мы можем оперировать только их модулями и не учитывать направления векторов. Пусть M – масса небесного тела и D – расстояние до Земли. Вычислим силу, с которой небесное тело действует на тело массой δ m в точке A или B. Между центром Земли O и точкой A или B расстояние до небесного тела претерпевает относительное изменение, равное R З / D , где R З – радиус Земли. Относительное изменение обеих сил F 1 и F 2 между точкой O и точкой A или B пропорционально этой величине. Итак, в точке O модули обеих сил равны GM δ m / D 2. Изменение этой величины при перемещении в точку A или B, следовательно, пропорционально GM δ mR З / D 3. Соответственно, пропорциональным GM δ mR З / D 3оказывается и модуль равнодействующей силы F →= F → 1+ F → 2, называемой приливной силой (силы в A и B направлены в противоположные стороны). Точное вычисление показывает, что коэффициент пропорциональности оказывается равным 3.

Соответственно, если небесное тело – Солнце, то результирующая сила в точках A или B будет равна GM С δ mR З / D Л 3, а в случае Луны – GM Л δ mR З / D Л 3. Из приведенной выше таблицы видно, что сила воздействия Луны на поверхности Земли примерно в два раза больше силы воздействия Солнца.

Напротив, сила гравитационного притяжения Земли Луной намного слабее притяжения Земли Солнцем, поскольку сила, осуществляемая массой M на расстоянии D , пропорциональна M / D 2, а отношение M С / D С 2почти в 200 раз больше отношения M Л / D Л 2(см. таблицу). А что можно сказать о влиянии Солнца на движение Луны? Для этого надо сравнить M С / D С 2и M З / D Л 2, где M З – масса Земли. Это величины одного порядка (см. таблицу). Следовательно, воздействием Солнца на движение Луны пренебрегать нельзя [4] Martin C. Gutzwiller, Rev. Mod. Phys., 70, 589-639, 1998. .