Эрик Роджерс - Физика для любознательных. Том 3. Электричество и магнетизм. Атомы и ядра

1) Вычислите К для волн, которые дают дифракционный максимум под углом 50° при рассеянии на кристалле с межатомным расстоянием 2,15∙10 - 10м (sin 50°= 0,766).

2) Сравните полученный результат с предсказанной вами в пункте а) «длиной волны» использованных электронов.

Измерения показали, что интерференционная картина соответствует длине волны λ= h/ mv. Одновременно аналогичная проверка была проведена в Англии Г. Томсоном. С тех пор проводилось много измерений аналогичных дифракционных картин для потоков электронов, протонов, атомов и даже нейтронов. Эти картины показывают, что частицы движутся в направлении распространения волн. Волны сообщают нам, где мы сможем обнаружить частицы, [Никаких исключений в этом отношении мы не ожидаем. Убедившись в волновом поведении атомов, мы считаем, что оно свойственно также бейсбольным мячам и винтовочным пулям, но грубые оценки их длин волн даже при медленном движении показывают, что они (длины волн) слишком малы, чтобы их можно было измерить или как-либо заметить любые волновые эффекты.]

Наиболее яркую демонстрацию волновых эффектов придумал Г. Мёлленштедт. Он натянул чрезвычайно тонкую проволоку поперек пучка электронов, вылетающих из пушки. На удаленной фотопленке, регистрирующей поток, образуется тень проволоки. Затем проволоке сообщается малый положительный заряд. Электрическое поле этого заряда отклоняет поток электронов, проходящих по обе стороны от проволоки, поэтому тень исчезает, а вместо нее появляется «яркое» пятно в том месте, где перекрываются два потока, проходящих с двух сторон проволоки. В этом пятне видны полосы Юнга — места, где

«электроны + электроны = больше электронов»,

и другие места, где

«электроны + электроны = нет электронов».

В темных полосах отнюдь не происходит взаимного уничтожения электронов — просто они не могут туда попасть, поскольку волновая природа уводит их куда-нибудь в другое место. Эта техника весьма трудна — картину нужно увеличить линзами электронного микроскопа, — но результаты великолепны.

Посмотрите на фиг. 199–202 и сравните картину, образованную электронами, и аналогичную картину для световых волн.

Фиг. 199. Волны из двух когерентных источников образуют интерференционные полосы.

Фиг. 200. «Бипризма» из стекла преобразует источник света в два источника так, что создаются световые интерференционные полосы.

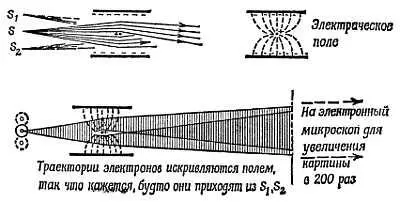
Фиг. 201. Эксперимент Мёлленштедта.

Для электронов электрическое поле возле положительно заряженной проволоки действует как «бипризма». Как и для фотонов, имеются «яркие» полосы в тех местах экрана, куда попадает много электронов, и «темные» полосы, куда попадает мало электронов, — направляющие «волны материи» создают интерференционную картину. Картина настолько мала, что ее приходится увеличивать линзами электронного микроскопа, а затем еще увеличивать с помощью оптики.

Фиг. 202. а — интерференционная картина, образованная видимым светом (увеличено в 30 раз).

Фотографию сделал Генри А. Хилл из Принстонского университета;

б— интерференционная картина, образованная электронами (увеличено в 5000 раз).

Фотография Г. Мёлленштедта и X. Дюкера из Тюбингенского университета. Эксперимент опубликован в журнале «Zeitschrift fur Phisik», том 145, 1956.

Сложный конфликт

Идею дуализма «волна — частица» трудно воспринять для света, но еще труднее — для атомов, электронов и всех кусочков вещества. Свет, проходящий через пару щелей в стенке, образует на удаленном экране интерференционные полосы Юнга. Но его энергия, очевидно, переносится пулеподобными квантами, большая часть которых попадает на яркие и лишь малое число квантов — на темные полосы. Если через две щели проходит поток электронов [199], снова получается интерференционная картина, так что каждый индивидуальный электрон должен каким-то образом пройти через обе щели [200]. Его волна должна проходить через обе щели, иначе как же получится интерференционная картина? Но как это может сделать пуля?

Волновые пакеты

По отношению к этому парадоксу де-Бройль выдвинул некоторые утешительные соображения — но его аргументы сложны и требуют математики в большей мере, чем мы здесь дадим, Его идея состояла в следующем: представлять волны, соответствующие фотонам или частицам вещества, как компактную группу мелких волн, подобную всплеску на воде, который можно создать одиночным шлепком по поверхности воды в ванне или бассейне.