Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

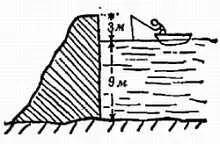
Фиг. 85. К задаче 4.

1) Можно найти общий вес воды, удерживаемой дамбой. Для этого надо использовать величину 2,93 км. Почему для расчета давления на дамбу это значение не нужно? (Другими словами, почему давление воды будет таким же, если вода простирается только на 1,93 км?)

2) Воздух давит? на открытую внешнюю часть дамбы. Это давление прибавляется также к давлению воды на внутреннюю поверхность дамбы.

Таким образом, при определении сил, опрокидывающих дамбу, эти два давления компенсируются. Поэтому в приведенных вычислениях атмосферным давлением можно пренебречь. Вычислите:

а) давление на открытой поверхности воды (ответ: нуль);

б) давление на дне водоема;

в) среднее давление на участке от верхнего уровня воды до дна (руководствуйтесь здравым смыслом);

е) общую силу, с которой вода давит на дамбу.

[ Указание : (давление) = (сила)/(площадь); (сила) = (давление)∙(площадь). Для расчета силы используйте среднее давление.]

Задача 5 (трудная)

Дамба построена слишком низкой, так что уровень воды оказался на 60 см выше верхнего края дамбы и вода переливается через дамбу (фиг. 86). Ширина дамбы 30 м, высота 12 м, а высота воды за дамбой 12,16 м. Следуя ходу вычислений задачи 4 , найдите общую силу, действующую на эту дамбу. (Пренебрегите всеми незнакомыми вам изменениями давления, обусловленными быстрым движением воды, например «эффектом Бернулли».)

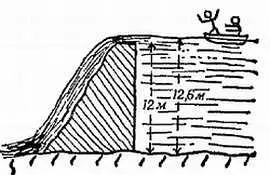
Фиг. 86. К задаче 5.

Законы давления (согласно Паскалю )

В покоящейся жидкости [53] Если жидкость движется, то нужно учитывать дополнительные факторы, например трение и «эффекты Бернулли» (см. гл. 9 ). давление подчиняется следующим правилам.

I. Давление одинаково по всему дну прямоугольного сосуда с жидкостью. В более общей форме давление одинаково во всех точках, которые находятся на одном и том же уровне в одной и той же жидкости (или газе).

II. Давление жидкости на любую поверхность направлено перпендикулярно к ней. (Водолаз, который держит в руке монету, убеждается, что независимо от того, как повернута монета, давление оказывается перпендикулярным к ее поверхности.)

III. В любой точке жидкости давление действует одинаково во всех направлениях. (Водолаз, который держит в руке монету, убеждается, что давление на монету одинаково независимо от того, в какую сторону она повернута.)

IV. Давление передается без потерь внутри жидкости из одного места в другое. (Если надавить на поршень гидравлической системы, то созданное давление передается на каждую стенку и на каждый другой поршень в системе.)

V. Разность давлений между любыми двумя точками в жидкости равна произведению h ∙ d , где h — разность уровней по вертикали, и d — плотность жидкости. На этом основан простой способ измерения давлений, который описан ниже.

Алгебраический вывод I и V законов давления

Закон I. Давление одинаково по всему дну прямоугольного сосуда с жидкостью. Давление на любой участок дна можно рассчитать следующим образом.

Выберем участок площадью А см 2.

Найдем вес вертикального столба жидкости, который опирается на основание А , т. е. силу притяжения, которая действует на эту часть жидкости (фиг. 87). Затем, чтобы найти давление, разделим этот вес на площадь основания А :

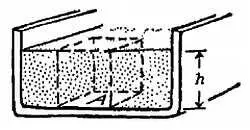
Фиг. 87. Закон I.Давление одинаково по всему дну прямоугольного бака с жидкостью.

ОБЪЕМ СТОЛБА = ВЫСОТА ∙ ПЛОЩАДЬ = h∙ А,

МАССА ЖИДКОСТИ В ЭТОМ СТОЛБЕ = ОБЪЕМ ∙ (МАССА / ОБЪЕМ) = ОБЪЕМ ∙ ПЛОТНОСТЬ = hА∙ d.

При применении «плохих» единиц (таких, как кГ) масса столба жидкости, выраженная в кг, численно равна весу жидкости в единицах кГ. Таким образом,

ДАВЛЕНИЕ р= СИЛА / ПЛОЩАДЬ = ВЕС СТОЛБА / ПЛОЩАДЬ ОСНОВАНИЯ = hAd/ A= hd

Итак, давление на любую площадь основания равно произведению

ГЛУБИНА ЖИДКОСТИ ∙ ПЛОТНОСТЬ

и не зависит от размера площади .

Если мы хотим выразить вес в «хороших» единицах, например в ньютонах, то должны умножить массу на ускорение силы тяжести g (9,8 ньютон/кг). Тогда