Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

б) Представьте себе, что проход между рифами идет в северном направлении, скорость течения равна 5 м/сек, направлено оно на восток, а скорость, сообщаемая судну винтом, равна 9 м/сек. Постройте график и покажите направление, в котором штурман должен, вести судно по компасу.

в) Представьте себе, что проход лежит к северу, а скорость течения равна 5 м/сек, направлено оно на восток. Докажите, что судно можно провести через проход только в том случае, если судовой двигатель позволяет развить скорость больше 5 м/сек.

Влияет ли порядок, в котором складываются векторы, на сумму?

Складывая векторы один за другим по правилу многоугольника, можно было бы располагать их в другом порядке, скажем A, D, С, В …, а не А, В, С, D …, в результате чего получим другой многоугольник. Получим ли мы ту же векторную сумму?

Приводимая ниже задача дает ответ на этот вопрос.

Задача 10

На фиг. 51 показано несколько векторов А, В, С, D, E , которые все проведены, из одной точки О . Сложите эти векторы по правилу многоугольника, т. е. проводя каждый последующий вектор из конца предыдущего, следуя данным ниже указаниям. Приведенный здесь рисунок слишком мал для точного выполнения чертежа и измерений, поэтому прежде всего воспроизведите его в большем масштабе на листе миллиметровки так, чтобы каждой клетке соответствовал квадрат со стороной 2 см. Затем к вектору А , который уже проведен, прибавьте В , затем С , затем D , затем Е , проводя каждый из прибавляемых векторов из конца предыдущего. Для этого вам придется перенести вектора В, С, D, Е при помощи какого-нибудь способа проведения параллельных прямых. (Воспользуйтесь либо данными, взятыми из разграфленной сетки фиг. 51, либо способом, показанным на фиг. 50.)

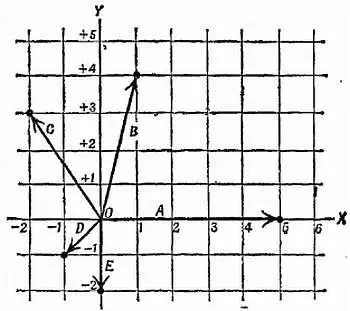
Фиг. 51.К задаче 10.

Проведите отрезок, выражающий сумму. Измерьте и запишите его величину. Чтобы определить направление суммы, нужно либо измерить какой-то угол, либо найти наклон отрезка, выражающего сумму. Испробуйте оба способа следующим образом:

а) Измерьте и запишите угол между суммой и самым первым вектором А .

б) Проведите две взаимно перпендикулярные оси ОХ и ОY , направив ось ОХ вдоль вектора А . Затем опустите перпендикуляр h из конца векторной суммы на ось ОХ (точно проводить этот перпендикуляр не нужно, можно просто измерить его длину). Измерьте высоту h и длину основания Ь , отсекаемого перпендикуляром на оси ОХ . После этого вычислите отношение (высота h )/(основание b ), которое называется наклоном отрезка R . Это позволит нам задать В , как вектор, величина которого равна…? а направление имеет наклон…?

Задача 11. Сумма однозначна

Получится ли иная векторная сумма, если складывать векторы в другой порядке? Проделайте снова задачу 10 на листе миллиметровки; начните, как и раньше, с вектора А , но прибавляйте к нему остальные векторы в другой последовательности: В, Е, D, С . Определите величину и направление суммы в этом случае.

Задача 12. Некоторые соображения по поводу сложения векторов

Представим себе векторы А, В, С, D, E в задаче 10 как перемещений, которые корабль должен совершить одно за другим. Представим себе оси ОХ, OY как направления восток и север, определяемые по компасу. Тогда одно перемещение, скажем В , переносит нас на некоторое расстояние к северу и на некоторое расстояние к востоку. Мы можем сказать, что перемещение В изменяет наш курс на столько-тo к северу и на столько-то к востоку. Фактически, же мы представляем себе перемещение В расчлененным, на компоненты, северную и восточную. Это называется «разложением вектора В на северную и восточную компоненты.

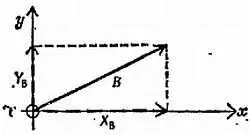
Фиг. 52. К задаче 12.

Разложение вектора на пару взаимно перпендикулярных «компонент» XB и YB, заменяющих этот вектор

Мы можем таким же образом разложить все векторы. Некоторые из восточных или северных компонент могут оказаться отрицательными. Сумму R тоже можно представить себе разложенной на восточную и северную компоненты. Когда мы складываем векторы, А, В …, то каждый из них вносит свою долю в изменение курса к востоку и к северу.