Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Алгебраический- анализ. Начертите на разграфленной бумаге с координатами х и у воображаемую траекторию летящего камня и найдите ее уравнение. Предположим, что камень брошен горизонтально из начала координат (0, 0) со скоростью 5 м/сек. Тогда за каждую секунду камень перемещается в горизонтальном направлении на 5 м. По прошествии t сек после начала движения камень переместится в горизонтальном направлении на 5t м, поэтому можно записать

РАССТОЯНИЕ, ПРОЙДЕННОЕ В ГОРИЗОНТАЛЬНОМ НАПРАВЛЕНИИ, х= 5∙ tм.

Через t сек камень, падая из состояния покоя, пройдет по вертикали расстояние у , определяемое формулой

РАССТОЯНИЕ, ПРОЙДЕННОЕ ПО ВЕРТИКАЛИ, y= 1/ 2УСКОРЕНИЕ t 2= 1/ 2(9,8)∙ t 2 = 4,9∙ t 2 м

Эти формулы справедливы для любой стадии движения камня по его криволинейной траектории, поэтому мы можем записать

x= 5∙ t

y= 4,9∙ t 2

Чтобы найти одно уравнение, описывающее траекторию движения, зададим себе вопрос: «Какое соотношение между х и у обеспечивает выполнение обоих приведенных выше требований на каждом этапе движения камня?» Для любой произвольно выбранной точки на траектории значения ее координат х и у должны удовлетворять обоим приведенным выше уравнениям для соответствующего значения t . Это значение t должно быть одинаковым в обоих уравнениях — ведь это время, когда камень достигает выбранной точки.

Поэтому мы можем избавиться от t , выразив из одного уравнения t и подставив полученное выражение в другое уравнение. Проделаем это.

Уравнение x= 5∙ tдает t= x/5; подставляя выражение х /5 вместо t в уравнение y= 4,9∙ t 2, получаем у= 4,9∙( х/5) 2, или у= (4,9/25)∙ x 2.

Уравнение траекторий движения камня будет тогда иметь вид у= 0,196∙ x 2.

В более общем случае, если камень брошен горизонтально с начальной скоростью v горм/сек и падает с вертикальным ускорением g м/сек на сек, то

x= v гор tи y= 1/ 2 gt 2

Следовательно,

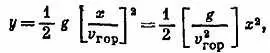
т. е. у= (постоянная) x 2, поскольку 1/ 2 g/ v 2 гop— постоянная величина.

Это уравнение параболы [34] Прежде парабола определялась как одна из кривых, получающихся при сечении конуса плоскостью. Сейчас параболу часто определяют как кривую, описываемую уравнением y = (постоянная)∙ х 2 , или у ~ x 2 . В одном из разделов аналитической геометрии показывается, что алгебраическое и геометрическое определения эквивалентны.

Воспользовавшись подобным уравнением, можно построить на клетчатой бумаге превосходные графики параболы. Постройте на бумаге с сантиметровыми клетками кривую, описываемую уравнением y = 1/ 2 x 2, взяв х = — 4, —3, —2, —1, 0, 1, 2 см и т. д.

Попытайтесь подогнать траекторию движения реального тела к этой кривой. Положите лист бумаги, на котором построена кривая, на чертежную доску, расположенную наклонно к плоскости стола, и скатывайте по ней шарик или держите лист бумаги отвесно и подбрасывайте перед ним какой-нибудь небольшой предмет.

Движение снаряда, выпущенного из пушки под углом к горизонту

Если снаряд выпущен не горизонтально, а вверх, под некоторым углом к горизонту, то его траектория по-прежнему будет параболой. Алгебраически это можно показать, используя уравнение s= v 0 t+ 1/ 2 gt 2,a не s= 1/ 2 gt 2. Таким образом, мы воспользуемся очевидной симметрией криволинейной траектории движения и можем сказать, что замедленное движение тела вверх до вершины траектории должно совпадать с ускоренным движением вниз, начинающимся от вершины, поэтому можно начертить всю траекторию, исходя из рассмотренной задачи движения снаряда, выпущенного горизонтально. Но все это лишь разумное предположение, хотя эксперимент подтверждает его. Можно рассуждать еще и так: двигаясь по ниспадающему участку траектории от вершины О , камень не может «знать», началось ли его движение в точке О или раньше, или позже. Поэтому камень, брошенный в какой-либо точке этого участка траектории, скажем в точке А , в сторону и вниз, должен двигаться по той же траектории, что и камень, брошенный горизонтально из вершины О , лежащей выше (фиг. 59).