Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Задача 17. Полицейская

Водитель автомобиля, въехав на мост, сильно превысил скорость. Машину занесло, она ударилась об ограждение и, разрушив его, упала в реку. Расстояние до поверхности воды составляло 4,9 м. Полиция установила, что машина упала в реку не вертикально под провалом в ограждении, а на расстоянии 19,8 м от него по горизонтали.

а) Оцените скорость, с какой шел автомобиль до катастрофы.

б) Как по-вашему, завышено или занижено полученное значение скорости? Объясните, почему.

в) Сформулируйте четко свойства падающих тел, которые вы использовали, производя вычисления по пункту ( а ).

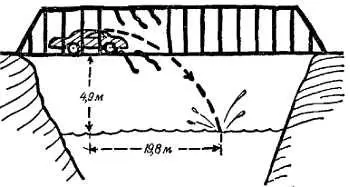
Фиг. 63. К задаче 17.

Задача 18. Поток электронов

Электрон, движущийся со скоростью 6 000 000 м/сек (совсем небольшая скорость для электрона) в горизонтальном направлении, попадает в область, где вертикальное электрическое поле сообщает ему ускорение, направленное вниз и равное 40 000 000 000 000 м/сек/сек, или 4∙10 13м/сек/сек. Область, в которой действует это поле, имеет протяженность 0,30 м в направлении первоначального движения. Таким образом, электрон движется по прямой в отсутствие поля, затем 0,30 м (по горизонтали) под действием вертикального поля, а потом снова попадает в область, где нет поля.

а) Как вы, полагаете, повлияет ли вертикальное ускорение на горизонтальное движение электрона?

б) Вычислите время, за которое электрон проходит через область, где действует поле.

в) Вычислите расстояние, которое пройдет электрон, совершая падение в области, где действует поле. (Это как раз то расстояние, которое экспериментатор измеряет, исследуя поведение электрона.)

г) Вычислите вертикальную компоненту скорости электрона в момент, когда он выходит из области, где действует поле.

д) Рассчитайте траекторию электрона и начертите (приблизительно) траекторию его движения до области, где действует поле, в этой области и возле нее.

е) Почему нет необходимости учитывать силу тяжести при решении этой задачи? (Она действует на электрон.)

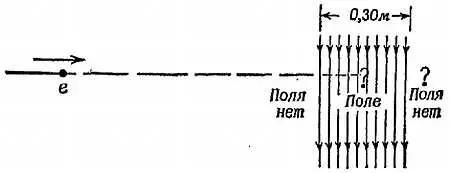
Фиг. 64. К задаче 18.

Задача 19. Дальность полета снаряда (задача решается с помощью алгебры и тригонометрии)

1) Из старинной пушки, ствол которой установлен под углом 45° к горизонту, выпущено ядро со скоростью 141,4 м/сек.

а) Разложите эту скорость на горизонтальную и вертикальную компоненты.

б) Вычислите, через сколько времени с момента вылета ядра оно упадет на землю.

в) Вычислите дальность полета.

2) Из старинной пушки выпущено ядро со скоростью v 0в направлении, которое составляет угол А к горизонту.

а) Разложите v 0на горизонтальную и вертикальную компоненты.

б) Вычислите время, в течение которого совершается вертикальное движение с момента вылета ядра до момента его падения на землю.

в) Вычислите расстояние, которое ядро проходит по горизонтали (т, е. дальность его полета).

3) Воспользовавшись методами тригонометрии или математического анализа, покажите, что при данной начальной скорости v 0дальность полета максимальна при А = 45°. (Вспомните, что 2sin x ∙cos x = sin 2 x .)

Задача 20. Измерение скорости летящего мяча

Физик хочет выяснить, с какой скоростью он может бросить бейсбольный мяч. Он бросает мяч горизонтально на высоте своего плеча, 1,2 м над поверхностью земли. Мяч падает на землю в 6 м от. того места, где стоит физик.

а) Чему равна начальная скорость мяча? (См. задачу 17.)

б) При вычислениях для ответа на вопрос ( а ) необходимо, помимо всяких формул для ускоренного движения, воспользоваться важным общим принципом, касающимся движения тел (его сформулировал Галилей). Что это за принцип?

в) Вместо того чтобы бросить мяч, наш физик бежит сам со скоростью, вычисленной в пункте ( а ), неся мяч на высоте плеча. На бегу он выпускает мяч, и мяч падает. Опишите, подумав как следует, траекторию падающего мяча:

Какой ее видит неподвижный наблюдатель?

Какой ее считает бегущий физик?

Задача 21

Автомобиль, движущийся со скоростью 20 м/сек (свыше 70 км/час) по горизонтальному участку горной дороги, делает неудачный поворот и падает в снежный сугроб с высоты 80 м (по вертикали).

а) Сколько времени продолжалось падение автомобиля?