Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Скорость

Направление перемещения имеет столь же важное значение, как и величина. В физике скорость связывают с определенным направлением . Скорость обладает обоими качествами: величиной и направлением [30] В обиходном языке, говоря о скорости, имеют в виду, насколько быстро движется предмет по какой-либо траектории — прямолинейной или искривленной. В физике скорость — это перемещение за единицу времени в определенном направлении, представляющее собой вектор. Чтобы задать скорость, указывают число, единицу измерения и направление, например 15 км/час в северном направлении. . Подчиняются ли скорости правилу геометрического сложения? Или, как сказал бы ученый, являются ли скорости «векторами»?

Векторы (определение)

Векторы — это величины, складываемые геометрическим способом . Они называются «векторами» [31] Слово «вектор» происходит от латинского глагола, означающего «везти», «нести» или «транспортировать». потому, что их можно охарактеризовать, проведя отрезок прямой, показывающий как величину вектора (в некотором масштабе), так и его направление.

Правило сложения двух векторов

Геометрическое сложение описывается следующим правилом. (Согласно определению векторов, оно автоматически применимо к ним.)

Чтобы сложить два вектора, выбирают подходящий масштаб и вычерчивают их в этом масштабе из одной точки, а затем строят на складываемых векторах параллелограмм. Тогда сумма векторов будет изображаться диагональю параллелограмма, соединяющей исходную точку с противолежащей вершиной.

При таком способе сложения сумма нескольких векторов определяется как единственный вектор, который может заменить первоначальные векторы, или производит такой же физический эффект.

Подобно тому как векторы А и В дают при сложении сумму R 2(фиг. 45), можно сложить векторы А и В и С , прибавив С к R 2, в результате чего получим вектор R 3. Прибавляя далее вектор D , получаем R 4и т. д. Или, проще говоря, любое количество векторов можно складывать, проводя следующий прибавляемый вектор из конца предыдущего, как показано на фиг. 46 (этот рисунок представляет собой лишь упрощение фиг. 45, б ), и их сумма будет изображаться вектором, соединяющим исходную точку с конечной.

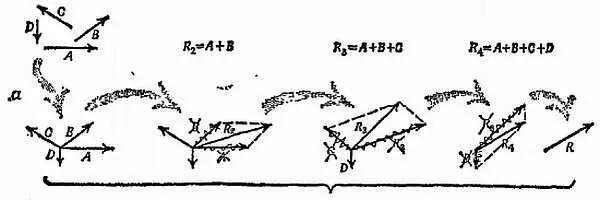
Фиг. 45. Сложение векторов путем построения параллелограмма.

а— этапы построения; б— результат построения.

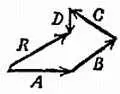
Фиг. 46. Сложение векторов путем построения многоугольника.

Какие величины относятся к векторам? Иначе говоря, какие величины складываются геометрически по правилу параллелограмма? Векторами являются перемещения, или, если называть их более строго, «направленные расстояния» или «смещения». Раз перемещения — векторы, то достаточно разделить их на промежуток времени, за который происходит перемещение, чтобы увидеть, что скорости — тоже векторы. Продолжая этот подход, мы видим, что ускорения — тоже векторы [32] Перемещение — это вектор. Скорость — это ведь перемещение в час, поэтому и скорость — вектор. Следовательно, изменение скорости (приращение или убыль скорости) — тоже вектор. Ускорение есть изменение скорости в час , поэтому и ускорение — вектор. . Нам встретятся и другие векторы, другие величины, которые нужно измерять с помощью приборов и которые подчиняются правилу геометрического сложения?

Здесь возникает важный вопрос: являются ли силы векторами, т. е. подчиняются ли они правилам геометрического сложения?

На этот вопрос нельзя ответить, просто подумав [33] Разве что мы готовы определить силы как величины, складываемые геометрически, а затем принять следствия этого определения при дальнейшем построении механики! . Ответ не очевиден и требует предварительного изучения (см. гл. 3 ).

Скаляры

Физические величины, которые имеют только величину и которым нельзя приписать никакого направления, называются скалярами ; хорошими примерами скалярных величин служат объем и температура. Существуют и такие вещи, которые не являются ни векторами, ни скалярами, скажем доброта, а также некоторые величины, этакие «сверхвекторы», называемые тензорами . Примером тензоров могут служить напряжения в деформированном твердом теле: давление, перпендикулярное к любой площадке образца, и срезающие усилия, действующие вдоль нее. Более сложные примеры встречаются в математической теории относительности. Например, мы будем рассматривать количество движения m vкак вектор с тремя компонентами: m v x, m v y, m v z, а кинетическую энергию — как скаляр. Эйнштейн, придерживаясь обобщенного представления о пространстве-времени, предпочитал объединять количество движения и кинетическую энергию в «четырехвектор», т. е. с четырьмя компонентами: три для количества движения и одна для кинетической энергии.