Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Можно проделать эти перемещения в другом порядке и прийти в тот же пункт назначения. Если бы вы смогли как-то проделать оба перемещения одновременно, то пришли бы в ту же конечную точку. В самом деле, это можно проделать, если приспособить ковер, который передвигался бы по полу при помощи электромотора.

Тогда, став на ковер (на фиг. 38 показан игрушечный автомобиль на коврике), можно было бы включить мотор, чтобы он протащил ковер на 4 шага вправо, а самому в это время сделать 3 шага вперед. По отношению к ковру вы сделаете только 3 шага вперед. С высоты птичьего полета покажется, что вы проделываете оба перемещения одновременно и приходите в тот же пункт назначения, как если бы вы сперва проделали одно перемещение, а потом другое.

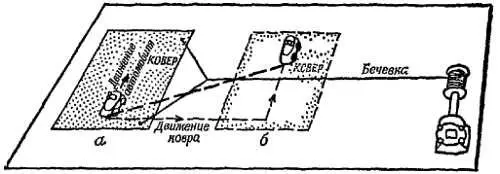
Фиг. 38. Сложение движений.

Игрушечный автомобиль движется по ковру, а ковер в это время тянет по полу электродвигатель. Движение автомобиля по отношению к полу совершается по диагонали.

Какое единственное перемещение могло бы заменить эти два, проделанные одновременно или по отдельности, и привести вас в тот же пункт назначения? Простое перемещение по прямой линии из исходной точки в конечную. Это перемещение называют суммой обоих перемещений . Если начертить перемещения в масштабе на бумаге, как на фиг. 39, то однократным перемещением, которое заменило бы оба перемещения (если бы они были сделаны по отдельности), будет перемещение R .

Фиг. 39. Сложение перемещений, происходящих под прямым углом.

Если перемещения совершаются не под прямым углом, то применимо такое же изображение в масштабе, как показано на фиг. 40.

Фиг. 40. Сложение перемещений.

Если перемещения совершаются одновременно (так бывает, когда полет самолета происходит при наличии ветра) мы можем по-прежнему считать, что сначала происходит одно перемещение, а потом другое, и прийти к результирующему перемещению R (фиг. 41).

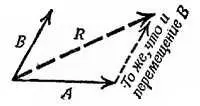
Фиг. 41. Сложение перемещений.

Мы находим результирующее перемещение, беря сначала одно перемещение, а затем другое, как показано на фиг. 42, а или б . Объединяя обе эти фигуры (фиг. 42, в ), мы видим, что результирующее перемещение дается диагональю параллелограмма, сторонами которого служат первоначальные перемещения.

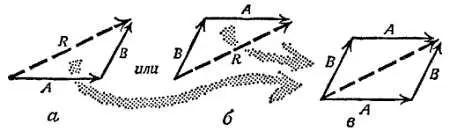
Фиг. 42. Сложение перемещений.

Это правило для сложения перемещений несомненно верно; в этом нас убеждает здравый смысл, основанный на опыте, приобретенном начиная с раннего детства.

Это правило можно обратить и разложить перемещение R на компоненты А и В . Эти компоненты — одна из возможных пар перемещений, которые вместе дают R . Существует бесконечное множество таких пар, каждая из которых дает в сумме одно и точке перемещение R .

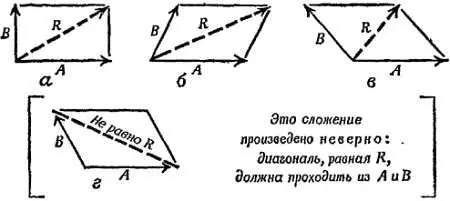
Фиг. 43. Примеры сложения перемещений по правилу параллелограмма.

Задача 6

а) На фиг. 44, а изображено перемещение R , разложенное на две компоненты А 1 и В 1 ; на фиг. 44, б показано то же самое перемещение R , разложенное на другую пару компонент А 2 и В 2 . Скопируйте эти рисунки и добавьте к ним еще несколько, на каждом из которых было бы изображено то же самое перемещение R , разложенное на другие компоненты: А 3, В 3, А 4, В 4 и т. д.

Фиг. 44. Вектор Rможно разложить на компоненты A 1и B 1, A 2и В 2или на другие пары компонент. Компоненты вектора Rне обязательно должны составлять между собой угол 90°.

б) Покажите, что компоненте А можно придать любое направление и любую величину и при этом найти такую компоненту В , которая в сумме с А даст R . (Это равносильно вычитанию векторов R-А , которое находит применение в физике и встретится нам в дальнейшем.)