а) Рассчитайте радиус наименьшего полукруга, который пилот маленького самолета может благополучно выполнить при скорости 300 фут/сек.
б) Как долго (примерно) будет двигаться по своему полукругу маленький самолет?
в) Вычислите радиус наименьшего полукруга, безопасного для самолета-преследователя,
г) Где будет находиться самолет-преследователь, когда маленький самолет уже закончит свой полукруг (обозначьте его путь на эскизе)?
Задача 9. Вариант вывода соотношения а = v 2/R (метод Ньютона)
Если тело движется по окружности от А до В , рассмотрите его как падающее тело с постоянным ускорением, направленным вниз. За время t оно пролетит с ускорением а расстояние h от той точки, в которой оно раньше покоилось.
а) Напишите уравнение для а через h и t , предполагая, что а постоянно.
б) Используя геометрическое свойство хорд круга, напишите уравнение, в котором h было бы выражено через другие измеряемые величины, приведенные на диаграмме.
в) Подставьте выражение для h в уравнение, полученное в вопросе ( а ).
г) Представьте, что В движется все ближе и ближе к А . Если В —> А , то горизонтальное расстояние х —> к дуге 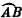 и, поскольку В —> А , хорда MN —> к диаметру 2 R . Внесите эти изменения в выражение для ускорения.
и, поскольку В —> А , хорда MN —> к диаметру 2 R . Внесите эти изменения в выражение для ускорения.
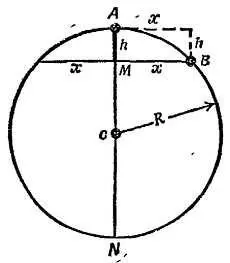
Фиг. 147. К задаче 9.
Задача 10. Центрифугирование
а) Центрифуга вращает пробирку по кругу со средним радиусом 1 фут со скоростью 5000 оборотов в минуту; содержимое пробирки находится при этом в силовом поле, во много раз большем g . Во сколько раз большем g ?
б) Образец мутной воды содержит частицы, размер которых примерно равен размерам, кровяных шариков (диаметр 10 -5м). Если пробирка расположена вертикально, частицы падают на дно с постоянной скоростью ~ 1/ 4дм/мин. Таким образом, объем жидкости высотой 4 дм полностью очистится примерно зa 1/ 4часа. (Эти частицы не осядут все на дно. Диффузия, связанная, с броуновским движением, поддерживает некоторое их количество во взвешенном состоянии.) За какое время тот же образец станет прозрачным в центрифуге, обеспечивающей ускорение, определенное в вопросе ( а )?
в) Белковые молекулы [диаметр которых в несколько сотен раз меньше диаметра частичек мути, о которых говорится в вопросе ( б ), но велик по сравнению с диаметром других молекул, скажем соли или воздуха] осаждаются в воде примерно в 300 000 раз медленнее, чем частички мути (вопрос б ). За какое время станет прозрачной помещенная в центрифугу 4-дюймовая пробирка, содержащая суспензию таких белковых молекул в воде?
г) Если, эту белковую суспензию не помещать в центрифугу, она никогда не станет прозрачной. Почему?
д) Если известна плотность частиц, то, исходя из спорости прояснения жидкости, можно определить диаметры частиц. (Сила торможения маленькой сферы пропорциональна ее радиусу и скорости.) Частички грязи (вопрос б ) могут быть измерены с помощью микроскопа, молекулы же белка увидеть невозможно. «Химические» измерения (осмотическое давление) показывают, что молекулы белка в 10 6раз тяжелее атома водорода. Какая важная информация о строении атома может быть получена с помощью измерений на центрифуге?
Глава 22. Исаак Ньютон (1642–4727)
«Если я видел дальше, чем другие, то лишь потому, что стоял на плечах гигантов».
Изречение, приписываемое Ньютону .
Жизнь и труды Ньютона
Ньютон родился в тот год, когда умер Галилей. Еще ребенком он увлекался опытами. И подобно Галилею и Тихо Браге мастерил занимательные игрушки, вроде водяных мельниц [86] Детские игры с кубиками, игрушками, печками, кранами позволяют получить определенный опыт — то, что мы называем здравым смыслом. Когда мы говорим «здравый смысл подсказывает нам это», мы часто апеллируем именно к такому опыту, даже иногда вопреки предрассудкам и традициям.
, и даже измерял «силу» ветра, замечая, насколько он мог прыгнуть в длину по ветру и против него. Поступив в школу, он поначалу не проявил особых успехов в изучении основного предмета — латыни, но вскоре обнаружил необыкновенные способности в математике.
Читать дальше

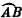 и, поскольку В —> А , хорда MN —> к диаметру 2 R . Внесите эти изменения в выражение для ускорения.
и, поскольку В —> А , хорда MN —> к диаметру 2 R . Внесите эти изменения в выражение для ускорения.







![Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]](/books/429584/jen-styuart-matematika-kosmosa-kak-sovremennaya-nau-thumb.webp)



