Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Венский вальс. Танцующая пара вращается вокруг общей оси, держась друг за друга (на одном или на обоих каблуках, фиг 128).

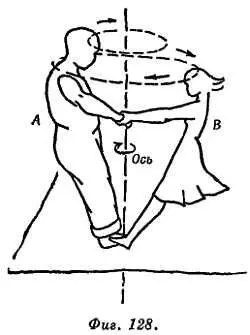
Партнеры тянут друг друга вовнутрь; эта тяга обеспечивает необходимые центростремительные силы. Даже если масса партнера А больше массы партнера В , натяжения одинаковы и противоположно направлены (третий закон Ньютона). Эта «система» так подбирает радиус своей орбиты, чтобы силы уравновешивались.

В результате партнеры вращаются вокруг оси, проходящей через их общий центр тяжести. А теперь найдем алгебраическое выражение для такого танцевального вращения (фиг. 129).

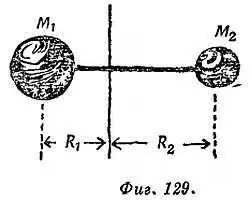
Предположим, что А и В имеют массы М 1и М 2и вращаются вокруг общей оси по окружности с радиусами R 1и R 2со скоростями v 1и v 2. Оба совершают один оборот за время Т . Тогда v 1= 2π R 1/ Tи v 2= 2π R 2/ T(т. е. v 1/ v 2= R 1/ R 2, хотя это и не необходимо). Обе центростремительные силы должны быть равны и противоположны друг другу, так как они обусловлены действием и противодействием танцоров. Таким образом,

М 1 v 2 1/ R 1= М 2 v 2 2/ R 2

или

М 1∙(2π R 1/ T) 2/ R 1= М 2∙(2π R 2/ T) 2/ R 2

т. е. М 1 R 1= М 2 R 2[сокращая ∙(2 π ) 2, Т 2и т. д.]. Тогда произведение ( масса )∙( расстояние от оси вращения ) будет одинаково для обоих партнеров. Поэтому более тяжелый партнер располагается на меньшем расстоянии от оси. Если вы посмотрите, что сказано о нахождении положения центра тяжести двух тел в пособиях по физике, то найдете, что если R 1и R 2измерять от оси, проходящей через центр тяжести М 1и М 2, то М 1 R 1должно быть равно М 2 R 2в соответствии со свойствами центров тяжести. Тогда для вращающихся систем М 1 R 1= М 2 R 2Именно поэтому танцующая вальс пара должна вращаться вокруг ее центра тяжести.

Подобное рассмотрение правильно описывает танцы с точки зрения физики, но вряд ли это практически полезна. Оно верно и в случае движения Луны и Земли и важно для понимания природы приливов. Астрономы используют его при рассмотрении движения двойных звезд. Вы встретите и другие примеры проявления центростремительной силы в астрономии и атомной физике.

Центробежная сила и средство от головной боли для инженеров

Движение по окружности требует реальной силы, направленной вовнутрь и производимой реальными внешними воздействиями. Представление о центростремительной силе поможет вам разобраться во всех проблемах, связанных с круговым движением. А вот что такое центробежная сила? Вы часто слышите это слово, даже сами его произносите, когда вам приходится вращать что-либо по кругу, вы найдете этот термин во многих книгах по физике. Существует множество мнений о том, что такое центробежная сила. Вы можете выбрать из них то, которое вам больше по вкусу.

МНЕНИЕ I: Центробежная сила — это ложная сила, представление о которой возникло на основе неправильного толкования запутанного взаимоотношения между воздействием, определяющим силу, и объектом приложения этой силы.

Если вы вращаете камень на веревке, ее натяжение тянет вашу руку наружу с той же силой, с какой тянет и камень внутрь. Это — настоящая центробежная сила, действующая на вашу руку, но не на вращающийся камень. Вы ощущаете, что вашу руку что-то тянет наружу и говорите: «Я чувствую, что камень и веревка оттягивают мне руку. Это свидетельствует о том, что центробежная сила тянет камень и веревка передает действие этой силы». Вот тут вы и ошиблись. Не существует никакой силы, действующей на камень. На самом деле веревка, оттягивая вашу руку наружу, в то же время тянет камень вовнутрь. Существует лишь одна действительная сила — центростремительная, тянущая камень вовнутрь

Фиг. 130. Центробежная сила?

Представьте себе, что вы собрались посетить аттракцион в парке и покататься на вращающемся полу. Вы и ваш спутник входите в помещение и садитесь на неподвижный полированный пол. Зная, в чем суть представления, вы прижимаетесь покрепче к полу» Когда пол начнет вертеться, вам покажется, будто какая-то неведомая сила отбрасывает вас от центра, и если бы не сцепление с полом, под действием этой силы вы стали бы скользить к ограждению.