Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Ньютон, строя догадки о существовании всемирного тяготения, создал теорию, связывающую падение тел, движение Луны и движение планет с приливами и отливами и т. д. Он показал, что третий закон Кеплера (как и другие два его закона) с необходимостью следуют из этой теории. Таким образом, закон R 3 /T 2 можно считать «верным» согласно обоим определениям: и по общей применимости , и по согласию с теорией . Он мог оказаться «неверной» догадкой, ожидающей, подобно закону «пяти правильных многогранников», большего количества данных, чтобы быть опровергнутым, или теории, которая не могла бы его «предсказать» [49] Ученые пользуются в этом случае словом «предсказать», хотя этот термин нельзя считать удачным. Здесь он означает «привести в соответствие с другими областями науки». .

Воображаемая «Задача Кеплера»

Чтобы судить о том, сколь сложно исследование, подобное тому, которое выполнил Кеплер, попробуем решить аналогичную задачу, пользуясь воображаемыми данными и воображаемыми соотношениями. Предположим, что вы придумали некую задачу и вам известна схема, по которой вы ее составили. Предложите мне найти эту схему. Вы предоставляете в мое распоряжение следующие данные

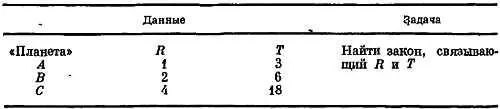
Вы знаете схему, так как сами ее придумали. (Эта система не подчиняется закону обратной пропорциональности квадрату расстояния, «планеты» не реальные!) Действительно, вы получите Т в соответствии с выбранным соотношением: T= R 2+ 2. Таким образом, если будет открыта новая планета D с R = 5, то для нее Т будет равно 5 2+ 2, т. е. 27. Предположим, что вы сообщили мне данные для планет А, В и С (а данные для D попридержали).

В поисках закона я пытаюсь найти такую алгебраическую комбинацию T и R, которая была бы одинаковой для каждой из этих планет . Начиная с планет А и B , я замечаю, что T / R = 3/1 для А и 6/2 для В , т. е. в обоих случаях это отношение одинаково. Надеясь, что нашел правильный закон, т. е. что T / R для всех планет одно и то же, я нахожу это отношение для планеты С . В этом случае оно равно 18/4, т. е. не равно первым двум. Поэтому я должен отвергнуть первую догадку. Пробуя другие комбинации, я нахожу еще несколько таких, которые дают одинаковые отношения для А и В , но не годятся для планеты C . Наконец, я нахожу, что соотношение между T и R будет одинаково для планет А и В , если я разделю 8 на R , прибавлю R , умноженное на 7, и вычту T , т. е. нахожу комбинацию 8/ R + 7 R — Т .

Для планеты А получим: 8/1 + 7 x 1–3 = 12.

Для планеты В получим: 8/2 + 7 x 2–6 = 12.

Для планеты С получим: 8/4 + 7 x 4 — 18 = 12, т. е. то же самое.

Итак, по-видимому, я нашел общий закон, которому подчиняются планеты А, В и С . Считая, что этот закон справедлив, я намереваюсь его опубликовать, но тут вы сообщаете данные о планете D: R = 5 и T = 27. Применяя свое правило к планете D , я получаю: 8/5 + 7x5 — 27 = 9,6.

Выяснив, что ваши данные не могут содержать ошибки, достаточно большой, чтобы объяснить расхождение между значениями 9,6 и 12,0, и начинаю все сначала. Если я достаточно терпелив и мне сопутствует удача, я могу прийти к следующей схеме: прибавить 2 к R 2и разделить полученный результат на Т . Тогда для всех четырех планет А, В, С и D получится один и тот же ответ, равный 1,000 [50] Можно разделить R 2 не на Т , а на 5 Т , тогда получим всюду 0,200, но в основном это дела не изменит. . Это позволяет думать, что найден правильный закон. Дальнейшие проверки при наличии большего числа данных подтверждают его правильность, и если этот закон будет находиться в соответствии с некой общей теорией, то я могу считать, что моя задача решена. Приведем таблицу, иллюстрирующую ход решения задачи.

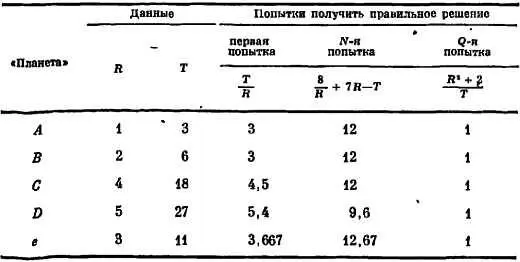
В последний момент была открыта еще одна «планета», е , таких малых размеров, что ее раньше не замечали. Ее данные тоже удовлетворяют окончательному правилу (в нашем примере в этом нет ничего удивительного, так как мы сами подогнали ее данные, заранее зная, какому правилу они должны удовлетворять) и находятся в противоречии с первыми попытками. Заметим, однако, что они почти точно соответствуют второй попытке, приводя к результату, равному 12,67. Если бы данные для планеты е были известны, когда я работал над своим вторым правилом, я мог бы поддаться искушению и решить, что 12,67 — значение, достаточно близкое к 12,00, и объяснить различие этих двух значений ошибкой эксперимента.