Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Убедившись в правильности своего предположения, он был так восхищен, что украсил свой чертеж изображением победоносной Астрономии на триумфальной колеснице, чтобы подчеркнуть значение полученного им доказательства (фиг. 82).

Наконец-то он определил, истинную орбиту Марса [46] Может показаться странным, что Кеплер не подумал об эллипсе ранее. Это был хорошо известный овал, исследованный греками как одно из сечений конуса. Нам-то это кажется теперь очевидным, когда мы знаем ответ. Следует еще помнить, что эллипсы не имели тогда столь большого значения и именно Кеплер создал им славу. [Эллипс легко нарисовать о помощью веревки или нитки и двух гвоздиков с широкими шляпками (фиг. 83). Если вы никогда не пробовали начертить таким образом эллипс, сделайте это. Забавный эксперимент продемонстрирует вам свойства эллипса.] Фиг. 83. Построение эллипса с помощью веревки и двух гвоздей. . Подобное же правило оказалось справедливым для Земли и других планет. В этом и состоит первый закон Кеплера, т. е. каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце .

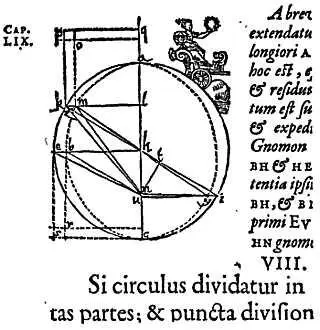
Фиг. 82. Диаграмма Кеплераиз его книги о Марсе.

Третий закон

Таким образом, с помощью таблиц Тихо Браге, благодаря бесстрашию, уму и неустанной работе Кеплер вывел два великих «закона». Он продолжал размышлять над одним из тех вопросов, которые интересовали его и ранее: какова связь между размерами орбит планет и длительностью их периодов обращения? Теперь ему были известны радиусы [47] Предполагая, что орбиты планет представляют собой круги, Коперник произвел грубые оценки их радиусов, Тихо Браге дал несколько более точные оценки. Эти значения были известны Кеплеру, когда он пытался построить свою странную схему из правильных многогранников, и их неточность позволила ему считать, что они; по-видимому, подтверждают его теорию. орбит, а периоды их обращения были известны с давних пор. (Как предполагали древние греки, планеты с большими периодами обращения имеют бóльшие орбиты.) Он был уверен, что между радиусом планеты и ее периодом обращения должно существовать определенное соотношение. Кеплер делал много попыток найти такое соотношение, но большинство попыток было безрезультатно, как и его планетная система из пяти правильных многогранников, другие же носили мистический характер.

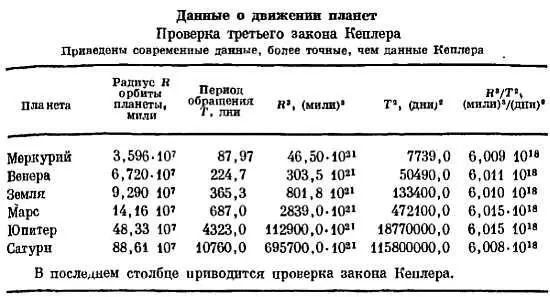
К счастью, связь между радиусами и периодами обращения действительно существует, и Кеплеру посчастливилось испытать радость открытия. Он нашел, что отношение R 3/ T 2одинаково для всех планет (здесь R — средний радиус орбиты планеты, а Т — период ее обращения, см таблицу).

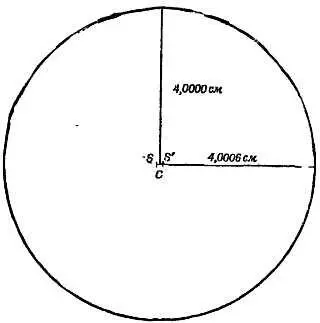
Фиг. 84. Орбита Земли (изображена в соответствующем масштабе).

Эксцентриситет орбит планет нашей системы в действительности очень мал. Орбиты почти круговые, однако на основе наблюдений Тихо Браге, Кеплеру удалось показать, что они представляют собой не круги, а эллипсы. Показана орбита Земли в масштабе. Минимальный радиус орбиты обозначен здесь как 4,0000 см, максимальный — 4,0006 см. Эксцентриситет орбиты Марса превышает эксцентриситет орбиты Земли более чем в тридцать раз, но и в этом случае радиусы относятся как 1,0048 к 1,000. Меркурий — единственная планета со значительно бóльшим эксцентриситетом, ее максимальный радиус относится к минимальному как 1,022 к 1,000. Даже этот эксцентриситет орбиты представляется малым, однако это значение оказывается уже достаточным, чтобы скорость Меркурия при его движении по орбите изменялась согласно предсказаниям релятивистской механики. Действительно, орбита Меркурия должна прецессировать, т. е. должна (очень медленно) вращаться. Прецессия орбиты Меркурия равна всего 1/80° в течение столетия — она была найдена и измерена задолго до того, как появилась теория относительности и было сделано это предсказание!

Фиг. 85. Соотношение между радиусом и «периодом обращениям для орбит различных планет.

Орбиты даны в грубом соответствии о масштабом

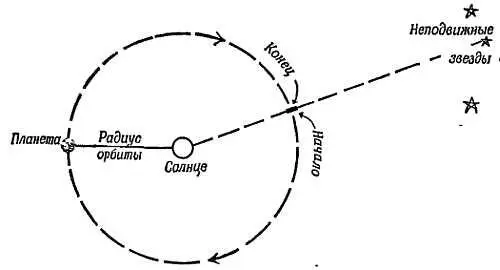
Фиг. 86. Период обращения планеты.