Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Фиг. 50. Система Птолемея.

Эта система очень точно описывает движения Солнца, Луны и планет.

Птолемей был вынужден считать, что плечо главного круга также вращается с постоянной скоростью. Этим плечом не мог быть проведенный из центра радиус, как в простой эпициклической схеме. Им не мог также быть и радиус, проведенный из точки Е . Но можно было спасти положение, взяв плечо, проведенное из равноудаленной точки Q , вращающейся с постоянной скоростью. Таким образом, для главного круга каждой планеты имелись три точки, расположенные близко друг к другу, каждая с характерными свойствами:

Е— Земля неподвижна

С— Центр главного круга с плечом СА постоянной длины

Q— Равноотстоящая точка с плечом QA , вращающимся с постоянной скоростью

Подбирая подходящие радиусы, скорости вращения и расстояние ЕС (= CQ ), Птолемей смог составить схему для всех планет (для Меркурия потребовался еще один дополнительный круг).

Для каждой планеты главному кругу придавался различный наклон и сам эпицикл имел наклон по отношению к главному кругу. Это была сложная система главных и вспомогательных кругов с различными радиусами, скоростями, наклонами и эксцентриситетами различной величины и направлений. Эта система, работающая подобно сложному передаточному механизму, позволяла из года в год точно предсказывать положения планет и определять эти положения в прошлом. Подобно хорошей системе механизмов, она была основана на простых принципах: круги с постоянными радиусами, вращение с постоянной скоростью, симметрия эквантов (равноотстоящих от центра точек: QC = CE ), постоянные наклоны кругов [27] Если эта настойчивость при подборе кругов покажется вам искусственной, то вспомните, что: А) ваши современные знания построены на том, что вам известно от других, Б) хотя эта модель кажется в настоящее время нереальной, она пригодна как метод анализа. Добавление одного круга к другому в греческой астрономии соответствует применению гармонического ряда (проекций круговых движений) для анализа сложных движений. Физики применяют в настоящее время такой «фурье-анализ», исследуя периодическое движение; анализируя звуки, предсказывая приливы и отливы, описывая поведение атома. Любое периодическое движение, каким бы сложным оно ни было, можно выразить в виде суммы простых гармонических движений. Каждое круговое движение в схеме Птолемея дает две такие компоненты — вверх и вниз, вправо и влево. Концентрические сферы Евдоксия можно также рассматривать как подобный анализ, но более сложный. С помощью той или другой схемы можно описать движение планет с любой точностью, если воспользоваться достаточным количеством компонент. и неподвижная Земля.

В « Альмагесте » Птолемей подробно описал схемы для каждой планеты и дал таблицы, по которым можно было определить движение каждого небесного тела. Книга была скопирована (разумеется, от руки), переведена с греческого на латинский, арабский и затем опять на латинский, по мере того как культура продвигалась на Восток, а затем опять в Европу. Существуют современные печатные варианты этой работы с переводами. Книга эта в течение столетий служила руководством для астрономов и справочником для мореплавателей. На основе содержащейся в ней информации развивалась астрология — специфическое скопление человеческих страхов, надежд, стремлений к наживе, которая нуждалась в подробных сведениях о положениях планет.

Схема Птолемея была эффективной и достаточно разумной. Мы можем сказать то же самое о нашей современной атомной и ядерной физике. Истинны ли эти теории? И древние греки, и современные ученые стали бы возражать против такой постановки вопроса; однако если бы вы предложили более простую и более плодотворную теорию, они приветствовали бы ее.

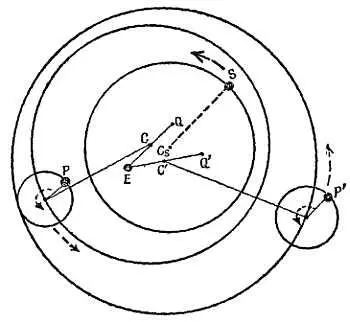
Фиг. 51. Система Птолемеядля Солнца Sи двух планет Ри Р'.

Е— неподвижная Земля; С— центр круга; Q— равноудаленная точка QС = СЕ .

Задача

Опишите своими словами и расскажите, используя диаграммы, о методе, применявшемся греками для определения

а) радиуса Земли;

б) расстояния от Земли до Луна;

в) расстояния от Земли до Солнца.