Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Прецессию было трудно наблюдать, пока Коперник, спустя 16 столетий, не упростил задачу, рассмотрев ее совершенно с иной точки зрения (см. гл. 16 ). Но и тогда она оставалась необъясненной и вне связи с другими небесными явлениями, пока Ньютон не нашел простого объяснения. Открытая как некий загадочный сдвиг, прецессия превратилась в признак тяготения.

Гиппарх оставил потомству прекрасный звездный каталог, схемы эпициклов и результаты наблюдений планет — бессмертный памятник астроному. Но все эти достижения вынуждены были лежать втуне два с половиной столетия, пока великий математик Птолемей не создал на их основе стройную теорию.

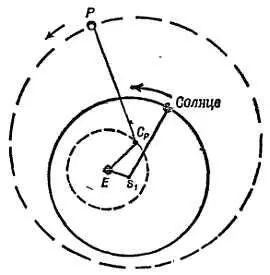
Фиг. 46. Схема эксцентрических орбит.

Показаны орбиты Солнцаи планеты Р

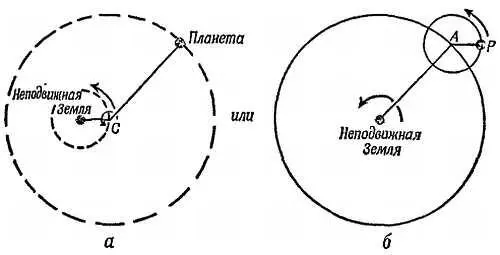
Фиг. 47. Схема эксцентрических орбит и схема эпициклов.

а— точка С и круг с радиусом орбиты планеты вращаются вокруг неподвижной Земли; б— Земля остается неподвижной в центре главного круга (деферент).

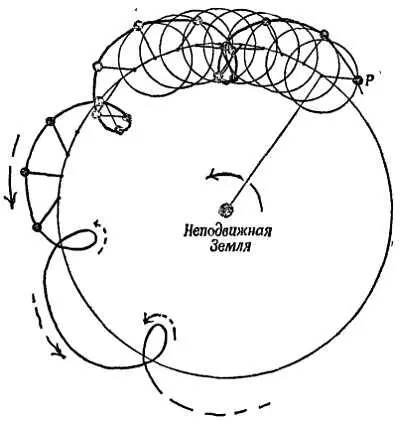
Фиг. 48. Траектория планеты в схеме эпициклов.

При комбинации двух круговых движений получается эпициклоида, по которой движется планета.

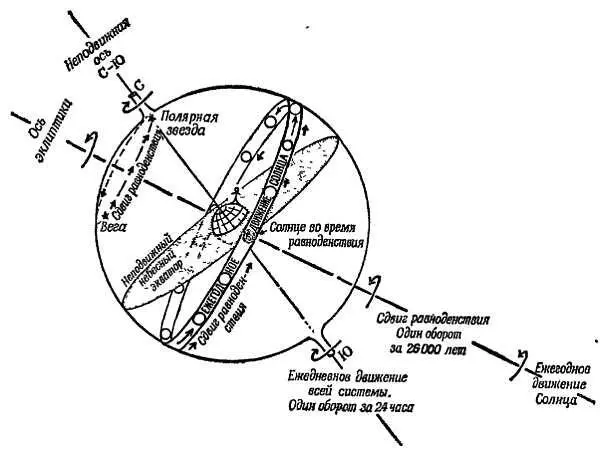
Фиг. 49. Прецессия равноденствий.

В добавление к суточному движению всего небесного свода вокруг оси, проходящей с севера на юг, и ежегодному движению Солнца по его эклиптическому пути в зодиаке Гиппарх открыл медленное вращение всей звездной картины вокруг оси эклиптики (перпендикулярной к зодиаку)

Птолемей(~ 120 г.) произвел «критическую переоценку наблюдений движения планет». Он собрал работы Гиппарха и его предшественников, добавил свои собственные наблюдения, создал первоклассную теорию и оставил великолепное изложение всей совокупности накопленных астрономических знаний, которая в течение последующих четырнадцати столетий играла решающую роль в астрономии. Положения Солнца, Луны и планет по отношению к неподвижным звездам были нанесены Птолемеем на карту, причем углы были измерены с точностью до доли градуса. Он смог поэтому разработать систему эксцентрических хрустальных сфер и эпициклов, которая не только была так усовершенствована, что точно описывала движение светил в прошлом, но с успехом позволяла предсказывать их будущие положения.

Птолемей создал великолепный математический аппарат, основанный на простых принципах, способный на протяжении веков предвосхищать явления. При этом он не рассматривал хрустальных сфер, а концентрировал свое внимание на вращающемся радиусе, (или «спице»), на конце которого находилась планета и который, вращаясь, как бы увлекал ее за собой. Он изложил всю свою систему движения светил — Солнца, Луны и планет — в трактате под названием «Альмагест».

Птолемей создал следующую картину: звездное небо — это сфера, вращающаяся вокруг неподвижной оси и совершающая полный оборот за 24 часа; Земля должна оставаться в центре небесной сферы, в противном случае звездная картина должна обнаруживать параллакс. Земля — это сфера, которая должна покоиться и тому есть ряд причин: если бы Земля двигалась, предметы, брошенные вверх, должны были бы отставать от нее. Солнце движется вокруг Земли согласно простой эпициклической схеме Гиппарха; Луна движется по более сложной эпициклоиде.

Исследуя «пять блуждающих звезд» — планеты, Птолемей обнаружил, что не может описать их движение простой эпициклоидой. Между теорией и наблюдением существовали расхождения. Он попытался создать схему эпициклов, в которой Земля находилась бы не в центре главного круга, а была бы несколько сдвинута относительно него, т. е. расположена эксцентрично.

Этого оказалось недостаточно, и Птолемей построил схему, в которой не только расположил Землю эксцентрично, но и сдвинул центр равномерного вращения в противоположную сторону. Он предложил схему, приведенную на фиг. 50, которая успешно описывала движения Солнца, Луны и планет. В его схеме С — центр главного круга, Е — Земля, расположенная эксцентрично; Q — точка, находящаяся на таком же расстоянии от С по другую сторону ( QC = CE ). Плечо QA вращается с постоянной скоростью вокруг Q , описывая равные углы за равные промежутки времени и неся на себе центр А маленького круга, эпицикла, который движется таким образом по главному кругу. Радиус эпицикла АР и, следовательно, планета Р , вращается с постоянной скоростью. Это была отчаянная, но успешная попытка подтвердить справедливость схемы кругов, вращающихся с постоянной скоростью.