Лев Ландау - Физика для всех. Молекулы

Рис. 2.11

Мы видим, что, например, в первых трех случаях . рисунок не обладает зеркальной плоскостью симметрии -- нельзя поставить вертикальное зеркало так,; чтобы одна часть рисунка была "отражением" другой части. Напротив, в случаях 4 и 5 имеются плоскости симметрии. В случаях 8 и 9 можно "установить" два взаимно перпендикулярных зеркала. В случае 10 имеются оси 4-го порядка, перпендикулярные к чертежу, в случае 11 - оси 3-го порядка. В случаях 13 и 15 имеются оси 6-го порядка и т. д.

Плоскости и оси симметрии наших рисунков выступают не поодиночке, а параллельными "семействами". Если мы нашли одну точку, - через которую можно провести ось (или плоскость) симметрии, то найдем быстро и соседнюю и далее на таком же расстоянии третью и четвертую и т. д. точки, через которые проходят такие же оси (или плоскости) симметрии.

17 типов симметрии плоского узора не исчерпывают, конечно, всего разнообразия узоров, составляемых из одной и той же фигурки; художник должен указать еще одно обстоятельство: как расположить фигурку по отношению к граничным линиям ячейки. На рис. 2.12 показаны два узора обоев с той же исходной фигуркой по различно расположенной по отношению к зеркалам. Оба эти узора относятся к случаю 8.

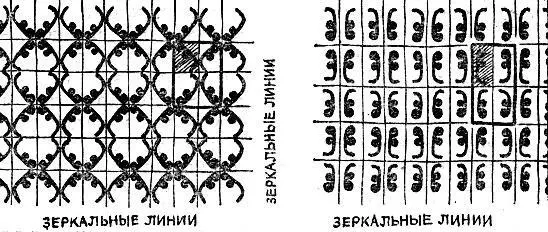
Рис. 2.12

Каждое тело, в том числе и кристалл, состоит из атомов. Простые вещества состоят из одинаковых атомов, сложные - из атомов двух или нескольких сортов. Предположим, что мы могли бы в сверхмощный микроскоп рассмотреть поверхность кристалла поваренной соли и увидеть центры атомов. Рис. 2.13 показывает, что атомы расположены вдоль грани кристалла, как узор обоев. Теперь вы уже можете легко понять, как построен кристалл. Кристалл представляет собой "пространственные обои". Пространственные, т. е. объемные, а не плоские элементарные ячейки - это "кирпичи", прикладыванием которых друг к другу в пространстве строится кристалл.

Рис. 2.13

Сколько же способов построения "пространственных обоев" из элементарных кусков? Эта сложная математическая задача была решена в конце прошлого века Евграфом Степановичем Федоровым. Он доказал,; что должны существовать 230 способов построения кристалла.

Все современные данные о внутреннем строении кристаллов получены при помощи рентгеноструктурного анализа, о котором мы расскажем в книге 4.

Существуют простые кристаллы, построенные из атомов одного сорта. Например, алмаз - это чистый углерод. Кристаллы поваренной соли состоят из ионов двух сортов: натрия и хлора. Более сложные кристаллы могут быть построены из молекул, которые в свою очередь состоят из атомов многих сортов.

Однако в кристалле всегда можно выделить наименьшую повторяющуюся группу атомов (в простейшем случае это будет один атом), иными словами, элементарную ячейку.

Размеры ячейки могут быть весьма различными. Наименьшие расстояния между соседними узлами (вершинами ячейки) встречаются у простейших кристаллов, построенных из атомов одного вида, наибольшие - у сложных кристаллов белка. Расстояния колеблются от 2-3 до нескольких сот ангстремов (стомиллионных долей сантиметра).

Кристаллические решетки очень разнообразны. Однако свойства, общие для всех кристаллов, безупречно объясняются решетчатым строением кристаллов. Прежде всего нетрудно понять, что идеально плоские грани - это плоскости, проходящие через узлы, в которых сидят атомы. Но узловых плоскостей можно провести сколько угодно по самым различным направлениям. Какие же из этих узловых плоскостей ограничивают выросший кристалл?

Обратим внимание прежде всего на следующее обстоятельство: разные узловые плоскости и линии заполнены узлами не одинаково плотно. Опыт показывает, что кристалл огранен плоскостями, которые гуще всего уееяны узлами, плоскости же пересекаются по ребрам, в свою очередь наиболее густо заселенным узлами.

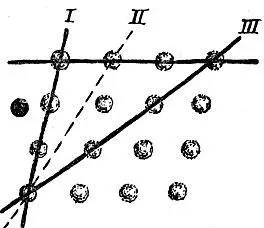
Рис. 2.14 дает вид кристаллической решетки перпендикулярно к ее грани; проведены следы некоторых узловых плоскостей, перпендикулярных к чертежу. Из сказанного ясно, что у кристалла могут развиться грани, параллельные узловым плоскостям I и III, и не будет граней, параллельных редко усеянным узлами плоскостям II.