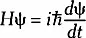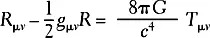Возможно, что в экспериментах будут получены данные, которые сильно пошатнут нашу веру в теорию струн. Структура теории струн гарантирует, что определённые базовые принципы должны соблюдаться во всех физических явлениях. Среди них унитарность (сумма вероятностей всех возможных результатов в данном эксперименте должна быть равна 1) и локальная Лоренц-инвариантность (в достаточно малой области справедлива специальная теория относительности), а также более технические свойства, такие как аналитичность и кроссинг-симметрия (результат столкновения частиц должен зависеть от импульсов частиц таким образом, чтобы удовлетворялся некоторый набор математических критериев). Если будет обнаружено — возможно, на Большом адронном коллайдере, — что любой из этих принципов нарушается, то примирить полученные данные с теорией струн станет трудной задачей. (Согласовать эти данные со Стандартной моделью физики частиц, которая также использует эти принципы, будет столь же проблематично; однако здесь спасает допущение, что при достаточно высоких энергиях Стандартная модель должна уступить место некой новой физике, поскольку она не включает в себя гравитацию. Но если мы получим данные, конфликтующие с любым из перечисленных выше принципов, это будет указывать на то, что новая физика — это не теория струн.)
Первое указание на парность форм Калаби — Яу возникло в работе Ланса Диксона, а также в независимой работе Вольфганга Лерхе, Николаса Уорнера и Кумруна Вафы. В моей работе с Роненом Плессером был предложен метод построения первого конкретного примера таких пар, которые мы назвали зеркальными парами , а соотношение между ними — зеркальной симметрией . Плессер и я также показали, что трудная задача, такая как определение числа сфер, которые можно упаковать в данную форму, неподъёмная при использовании одного из партнёров по паре, может стать гораздо легче на зеркальной форме. Этот результат был подхвачен Филиппом Канделасом, Ксенией де ла Осой, Полом Грином и Линдой Паркерс — они развили технику вычислений, основанную на равенстве, которое Плессер и я установили между «трудными» и «простыми» формулами. С помощью простой формулы они получили информацию о трудном партнёре, включая числа, связанные с упаковкой сфер, приведённые в основном тексте книги. За последующие годы зеркальная симметрия стала отдельной областью исследований, где было получено много важных результатов. Детальная история этого вопроса приведена в книге Шин-Туна Яу и Стива Надиса: Shing-Tung Yau and Steve Nadis, «The Shape of Inner Space». New York: Basic Books, 2010.
Классическая механика: 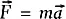 Электромагнетизм: d * F = * J; dF = 0. Квантовая механика:
Электромагнетизм: d * F = * J; dF = 0. Квантовая механика:
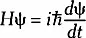
Общая теория относительности:
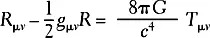
Я имею в виду постоянную тонкой структуры, α = e 2/ ħc , численное значение которой (при характерных энергиях электромагнитных процессов) примерно равно 1/137, что приближённо составляет 0,0073.
Согласно Виттену, когда константа связи в теории струн типа I становится большой, эта теория преобразуется в O-гетеротическую теорию с малой константой связи, и наоборот; теория типа IIB с большой константой связи преобразуется в себя, в теорию типа IIB, но с малой константой связи. В случае E-гетеротической и теории типа IIA ситуация более тонкая (более подробно см.: «Элегантная Вселенная», глава 12), но общая картина такова, что все пять теорий являются участниками целой сети взаимосвязей.
Для подготовленного читателя отметим, что особенность струн — одномерных объектов — состоит в том, что описывающая их движение физика основана на некоторой бесконечномерной группе симметрии. Так как при движении струна заметает двумерную поверхность, то струнный функционал действия, на основе которого выводятся уравнения движения, определяет двумерную квантовую теорию поля. Классически, такие двумерные действия являются конформно-инвариантными (инвариантными относительно сохраняющих углы растяжений двумерной поверхности), и при наложении некоторых ограничений (таких как число измерений пространства-времени, в котором движется струна) конформная симметрия может сохраняться на квантовом уровне. Конформная группа преобразований симметрии бесконечномерная и это существенно для математической согласованности пертурбативного квантового анализа движущейся струны. Например, бесконечное число возбуждений движущейся струны, которые иначе имели бы отрицательную норму (возникающую из отрицательного знака временной компоненты пространственно-временной метрики), может быть устранено с помощью преобразований «вращения» из бесконечномерной группы симметрии. Более подробно можно прочитать в книге: М. Green, J. Schwarz, and Е. Witten, «Superstring Theory». Vol. 1. Cambridge: Cambridge University Press, 1988.
Читать дальше

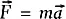 Электромагнетизм: d * F = * J; dF = 0. Квантовая механика:
Электромагнетизм: d * F = * J; dF = 0. Квантовая механика: