Chapter 29. The Tesseract
When Christopher Nolan told me he was going to use a tesseract in Interstellar , I was delighted. At age thirteen I read about tesseracts in Chapter 4 of George Gamow’s marvelous book One, Two, Three, …Infinity (Gamow 1947), and that had a major role in making me want to become a theoretical physicist. You can find a detailed discussion of tesseracts in The Visual Guide to Extra Dimensions (McMullen 2008). Christopher Nolan’s complexified tesseract is unique; there is not yet any public discussion of it anywhere, except in this book and others connected to the movie Interstellar .
In Madeleine L’Engle’s classic science fantasy novel for children, A Wrinkle in Time (L’Engle 1962), children travel via a tesseract—they “tesser”—to find their father. My own interpretation of this is a journey through the bulk, riding in the face of a tesseract, like my interpretation of Cooper’s trip from Gargantua’s core to Murph’s bedroom, Figure 29.4.
Chapter 30. Messaging the Past
For physicists’ current understanding of backward time travel in four spacetime dimensions without a bulk, see the last chapter of Black Holes & Time Warps (Thorne 1994), the chapters by Hawking, Novikov, and me in The Future of Spacetime (Hawking et al. 2002), and Time Travel and Warp Drives (Everett and Roman 2012). These are all by physicists who have contributed in major ways to the theory of time travel. For a historical account of modern research on time travel, see The New Time Travelers: A Journey to the Frontiers of Physics (Toomey 2007). For a comprehensive discussion of time travel in physics, in metaphysics, and in science fiction, see Time Machines: Time Travel in Physics, Metaphysics and Science Fiction (Nahin 1999). From Eternity to Here: The Quest for The Ultimate Theory of Time (Carroll 2011) is a wonderful discussion of almost everything physicists know, or speculate, about the nature of time.
I don’t know any good books or articles, for general readers, about time travel when our universe is a brane that lives in a higher dimensional bulk; but as I discuss in Chapter 30, Einstein’s laws extended to higher dimensions give basically the same predictions as without a bulk.
For some technical details of Cooper’s sending messages backward in time to Murph, see the appendix Some Technical Notes .
Chapter 31. Lifting Colonies off Earth
For Murph’s method (reducing G ) for lifting the colonies off Earth, in my interpretation of Interstellar , see my remarks about Chapter 25, above.
In the early 1960s, when I was a PhD student at Princeton University, one of my physics professors, Gerard K. O’Neill, was embarking on an ambitious feasibility study for colonies in space, colonies somewhat like the one we see at the end of Interstellar . His study, augmented by a NASA study that he led, resulted in a remarkable book, The High Frontier: Human Colonies in Space (O’Neill 1978), which I highly recommend. But do pay attention to the book’s introduction by Freeman Dyson, which discusses why O’Neill’s dream of space colonies in his lifetime was shattered, but envisions them in the more distant future.
The laws of physics that govern our universe are expressed in the language of mathematics. For readers comfortable with math, I write down a few formulas that come from the physical laws and show how I used them to deduce some things in this book. Two numbers that appear frequently in my formulas are the speed of light, c = 3.00 × 10 8meters/second, and Newton’s gravitational constant, G = 6.67 × 10 –11meters 3/kilogram/second 2. I use scientific notation so 10 8means 1 with eight zeros after it, 100,000,000 or a hundred million, and 10 –11means 0.[ten zeros]1, that is, 0.00000000001. I don’t aspire to accuracy any higher than 1 percent, so I show only two or three digits in my numbers, and when a number is very poorly known, only one digit.
Chapter 4. Warped Time and Space, and Tidal Gravity
The simplest, quantitative form of Einstein’s law of time warps is this: Place two identical clocks near each other, and at rest with respect to each other, separated from each other along the direction of the gravitational pull that they feel. Denote by R the fractional difference in their ticking rates, by D the distance between them, and by g the acceleration of gravity that they feel (which points from the one that ages the fastest to the one that ages the slowest). Then Einstein’s law says that g = Rc 2/ D . For the Pound-Rebca experiment in the Harvard tower, R was 210 picoseconds in one day, which is 2.43 × 10 –15, and the tower height D was 73 feet (22.3 meters). Inserting these into Einstein’s law, we deduce g = 9.8 meters/second 2, which indeed is the gravitational acceleration on Earth.
Chapter 6. Gargantua’s Anatomy
For a black hole such as Gargantua that spins extremely fast, the horizon’s circumference C in the hole’s equatorial plane is given by the formula C = 2π GM / c 2 = 9.3 ( M / M sun) kilometers. Here M is the hole’s mass, and M sun = 1.99 × 10 30kilograms is the Sun’s mass. For a very slowly spinning hole, the circumference is twice this size. The horizon’s radius is defined to be this circumference divided by 2π: R = GM / c 2 = 1.48 × 10 8kilometers for Gargantua, which is very nearly the same as the radius of the Earth’s orbit around the Sun.
The reasoning by which I deduce Gargantua’s mass is this: The mass m of Miller’s planet exerts an inward gravitational acceleration g on the planet’s surface given by Newton’s inverse square law: g = Gm / r 2, where r is the planet’s radius. On the faces of the planet farthest from Gargantua and nearest it, Gargantua’s tidal gravity exerts a stretching acceleration (difference of Gargantua’s gravity between the planet’s surface and its center a distance r away) given by g tidal = (2 GM / R 3) r. Here R is the radius of the planet’s orbit around Gargantua, which is very nearly the same as the radius of Gargantua’s horizon. The planet will be torn apart if this stretching acceleration on its surface exceeds the planet’s own inward gravitational acceleration, so g tidalmust be less than g : g tidal < g . Inserting the formulas above for g, g tidal, and R , and expressing the planet’s mass in terms of its density ρ as m = (4π/3) r 3ρ, and performing some algebra, we obtain 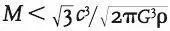 . I estimate the density of Miller’s planet to be ρ = 10,000 kilograms/meter 3(about that of compressed rock), from which I obtain M < 3.4 × 10 38kilograms for Gargantua’s mass, which is about the same as 200 million suns—which in turn I approximate as 100 million suns.
. I estimate the density of Miller’s planet to be ρ = 10,000 kilograms/meter 3(about that of compressed rock), from which I obtain M < 3.4 × 10 38kilograms for Gargantua’s mass, which is about the same as 200 million suns—which in turn I approximate as 100 million suns.
Using Einstein’s relativistic equations, I have deduced a formula that connects the slowing of time on Miller’s planet, S = one hour/(seven years) = 1.63 × 10 –5to the fraction α by which Gargantua’s spin rate is less than its maximum possible spin: 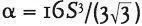 . This formula is correct only for very fast spins. Inserting the value of S , we obtain α = 1.3 × 10 –14; that is, Gargantua’s actual spin is less than its maximum possible spin by about one part in a hundred trillion.
. This formula is correct only for very fast spins. Inserting the value of S , we obtain α = 1.3 × 10 –14; that is, Gargantua’s actual spin is less than its maximum possible spin by about one part in a hundred trillion.
Читать дальше

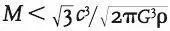 . I estimate the density of Miller’s planet to be ρ = 10,000 kilograms/meter 3(about that of compressed rock), from which I obtain M < 3.4 × 10 38kilograms for Gargantua’s mass, which is about the same as 200 million suns—which in turn I approximate as 100 million suns.
. I estimate the density of Miller’s planet to be ρ = 10,000 kilograms/meter 3(about that of compressed rock), from which I obtain M < 3.4 × 10 38kilograms for Gargantua’s mass, which is about the same as 200 million suns—which in turn I approximate as 100 million suns.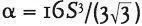 . This formula is correct only for very fast spins. Inserting the value of S , we obtain α = 1.3 × 10 –14; that is, Gargantua’s actual spin is less than its maximum possible spin by about one part in a hundred trillion.
. This formula is correct only for very fast spins. Inserting the value of S , we obtain α = 1.3 × 10 –14; that is, Gargantua’s actual spin is less than its maximum possible spin by about one part in a hundred trillion.










