Intermediate-Mass Black Holes in Galactic Nuclei
A 10,000-kilometer IMBH weighs about 10,000 solar masses. That’s ten thousand times less than Gargantua, but a thousand times heavier than typical black holes. These are the deflectors Cooper needs.
Some IMBHs are thought to form in the cores of dense clusters of stars called globular clusters, and some of them are likely to find their way into the nuclei of galaxies, where gigantic black holes reside.
An example is Andromeda, the nearest large galaxy to our own (Figure 7.4), in whose nucleus lurks a Gargantua-sized black hole: 100 million solar masses. Huge numbers of stars are drawn into the vicinity of such gigantic black holes; as many as a thousand stars per cubic light-year. When an IMBH passes through such a dense region, it gravitationally deflects the stars, creating a wake with enhanced density behind itself (Figure 7.4). The wake pulls on the IMBH gravitationally, slowing the IMBH down, a process called “dynamical friction.” As the IMBH very gradually slows, it sinks deeper into the vicinity of the gigantic black hole. In this manner, Nature could provide Cooper, in my interpretation of Interstellar , with the IMBHs that he needs for his slingshots. [19] The probability of finding IMBH’s at the needed locations and times is small, but in the spirit of science fiction, since it is within the bounds of physical law, we can utilize them.
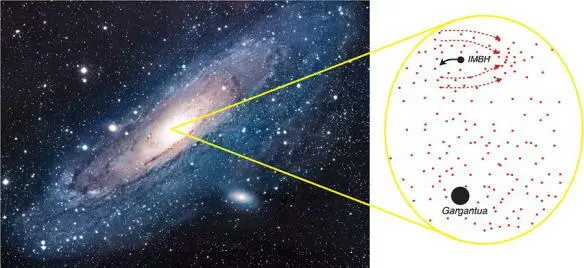
Fig. 7.4. Left : The Andromeda galaxy, which harbors a Gargantua-sized black hole. Right : The dynamical friction by which an IMBH will gradually slow down and sink into the vicinity of the gigantic black hole.
Orbital Navigation by Ultra-Advanced Civilizations: A Digression
The orbits of planets and comets in our solar system are all ellipses to very high accuracy (Figure 7.5). Newton’s laws of gravity guarantee and enforce this.
By contrast, around a gigantic, spinning black hole such as Gargantua, where Einstein’s relativistic laws hold sway, the orbits are far more complex. Figure 7.6 is an example. For this orbit, each trip around Gargantua would require a few hours to a few days, so the entire pattern in Figure 7.6 would be swept out in about a year. After a few years, the orbit would pass near most any destination you might wish, though the speed at which you arrive might not be right. A slingshot might be needed to change speed and make a rendezvous.
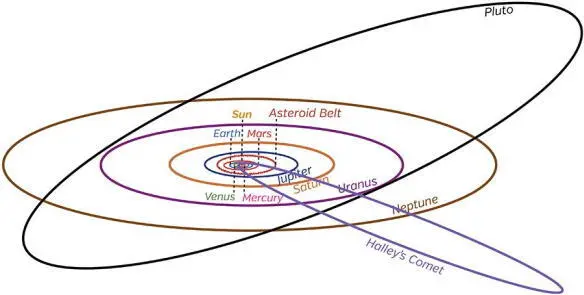
Fig. 7.5. The orbits of planets, Pluto, and Halley’s comet in our solar system are all ellipses.
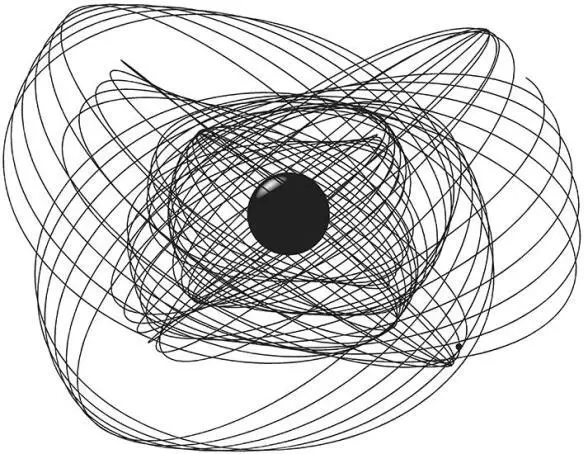
Fig. 7.6. A single orbit of a spacecraft or planet or star around a gigantic, fast-spinning black hole such as Gargantua. [From a simulation by Steve Drasco.]
I’ll let you imagine how an ultra-advanced civilization might use such complex orbits. In my science interpretations of the movie, for simplicity I mostly eschew them and focus primarily on circular, equatorial orbits (those of the parked Endurance , Miller’s planet, and the critical orbit), and on simple trajectories for the Endurance as it travels from one circular equatorial orbit to another. An exception is the orbit of Mann’s planet, discussed in Chapter 19.
NASA’s Gravitational Slingshots in the Solar System
Let’s return from the world of the possible (what the laws of physics allow) to hard-nosed, real-life gravitational slingshots in the comfy confines of our solar system (what humans have actually achieved as of 2014).
You may be familiar with NASA’s Cassini spacecraft (Figure 7.7). It was launched from Earth on October 15, 1997, with too little fuel to reach its destination, Saturn. The deficit was dealt with by slingshots: around Venus on April 26, 1998; a second slingshot around Venus on July 24, 1999; around Earth on August 18, 1999; and around Jupiter on December 30, 2000. Arriving at Saturn on July 1, 2004, Cassini slowed down with the aid of a slingshot around Saturn’s closest moon, Io.
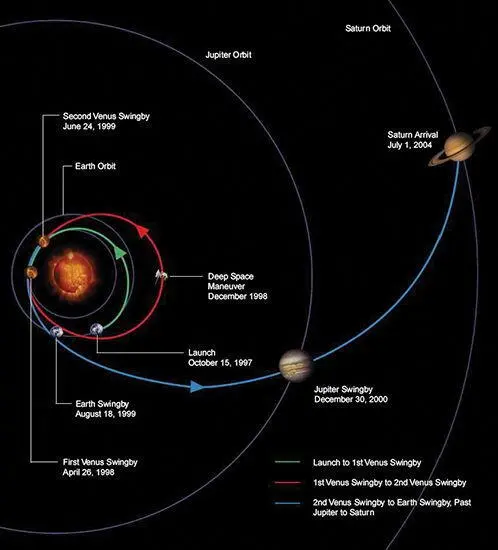
Fig. 7.7. The trajectory of Cassini from Earth to Saturn.
None of these slingshots looked like the ones I described above. Instead of strongly deflecting the spacecraft’s direction of motion, Venus, Earth, Jupiter, and Io deflected it only mildly. Why?
The deflectors’ gravity was too weak to produce a strong deflection. For Venus, Earth, and Io, the deflection was inevitably small because their gravity is intrinsically weak. Jupiter has much stronger gravity, but a large deflection would have sent Cassini in the wrong direction; reaching Saturn required a small deflection.
Despite the small deflections, Cassini got substantial kicks from the flybys, big enough to compensate for inadequate fuel. In each flyby (except Io), Cassini traveled behind the deflecting planet but at an angle, so the planet’s gravity optimally pulled Cassini forward, speeding it up. In Interstellar , the Endurance does a similar slingshot around Mars.
Cassini has been exploring Saturn and Saturn’s moons for the past ten years, sending back amazing images and information—a treasure trove of beauty and science. For a glimpse, see http://www.nasa.gov/mission_pages/cassini/main/.
By contrast with these weak slingshots in the solar system, Gargantua’s intense gravity can grab even objects moving at ultrahigh speeds and throw them around on strongly bent slingshots. Even a light ray. This produces gravitational lensing, the key to seeing Gargantua.
8
Imaging Gargantua

Black holes emit no light, so the only way to see Gargantua is by its influence on light from other objects. In Interstellar the other objects are an accretion disk (Chapter 9) and the galaxy in which it lives including nebulae and a rich field of stars. For the sake of simplicity, let’s include only the stars for now.
Gargantua casts a black shadow on the field of stars and it also deflects the light rays from each star, distorting the stellar pattern that the camera sees. This distortion is the gravitational lensing discussed in Chapter 3.
Figure 8.1 shows a rapidly spinning black hole (let’s call it Gargantua) in front of a field of stars, as it would appear to you if you were in Gargantua’s equatorial plane. Gargantua’s shadow is the totally black region. Immediately outside the shadow’s edge is a very thin ring of starlight called the “ring of fire” that I intensified by hand to make the edge of the shadow more distinct. Outside that ring we see a dense sprinkling of stars with a pattern of concentric shells, a pattern produced by the gravitational lensing.

Fig. 8.1. The gravitationally lensed pattern of stars around a rapidly spinning black hole such as Gargantua. When seen from far away, the shadow’s angular diameter, measured in radians, is 9 Gargantua radii divided by the observer’s distance from Gargantua. [From a simulation by the Double Negative visual-effects team.]
As the camera orbits around Gargantua, the field of stars appears to move. This motion combined with the lensing produces dramatically changing patterns of light. The stars stream at high speed in some regions, they float gently in others, and they’re frozen in still other regions; see the film clip on this book’s page at Interstellar.withgoogle.com.
Читать дальше


















