Кип Торн - Черные дыры и складки времени. Дерзкое наследие Эйнштейна

Обнаружив посредством таких измерений, что их вселенная искривлена, плоскатики могут начать строить предположения о существовании трехмерного пространства, в котором находится их двумерная вселенная или в которое она вложена.

Они могут назвать это трехмерное пространство гиперпространством и фантазировать о его свойствах. Например, они могут пред-положить, что оно плоское в евклидовом смысле, т. е. параллельные прямые в нем никогда не пересекаются.

Нам с вами представить такое гиперпространство совсем несложно — это наше обычное трехмерное пространство. Однако плоскатикам сделать это было бы очень непросто. Более того, у них не было бы никакой возможности проверить, существует ли это гиперпространство на самом деле, ведь ни выйти из своей двумерной вселенной, ни бросить взгляд наружу из нее они не могут. Для них гиперпространство навсегда осталось бы лишь гипотезой.

Это третье измерение гиперпространства не имеет никакого отношения ко времени плоскатиков, которое они также могли бы назвать третьим измерением. В общей сложности, размышляя о гиперпространстве, плоскатики оперировали бы четырьмя измерениями: двумя пространственными измерениями своей вселенной, одним временным и одним дополнительным пространственным измерением гиперпространства.

* * *

Мы с вами — объемные существа и живем в трехмерном пространстве. Если бы мы провели исследования геометрии нашего пространства внутри и вблизи звезды шварцшильдовской геометрии, мы обнаружили бы, что оно искривлено, подобно тому, как в нашем примере была искривлена вселенная плоскатиков.

Можно строить предположения о высших измерениях — плоском гиперпространстве, в которое вложено наше искривленное трехмерное пространство. Оказывается, такое гиперпространство должно быть шестимерным, чтобы в него можно было вложить искривленное трехмерное пространство, подобное нашему (а если вспомнить, что наша Вселенная имеет еще временное измерение, всего измерений оказывается семь).

Наглядно изобразить наше трехмерное пространство, вложенное в шестимерное гиперпространство, мне ничуть не легче, чем плоскатикам — свое двумерное, вложенное в трехмерное. Однако существует прием, который окажет нам неоценимую помощь (см. рис. 3.3).

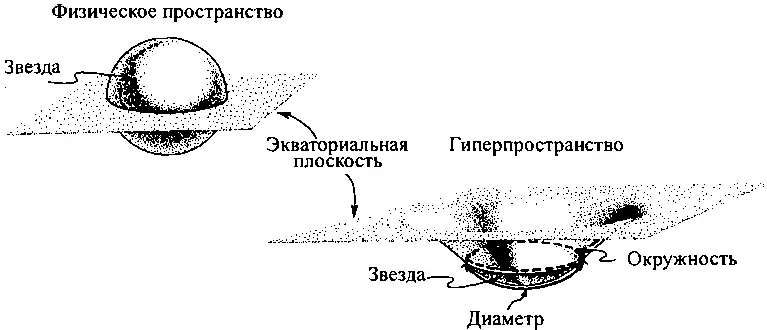
3.3. Кривизна трехмерного пространства внутри и вокруг звезды (слева вверху) и ее представление на вложенной диаграмме (справа внизу). Эта кривизна предсказывается шварцшильдовским решением уравнения Эйнштейна

Рис. 3.3 иллюстрирует мысленный эксперимент: тонкий лист разрезает звезду в плоскости ее экватора так, что совершенно одинаковые половинки звезды оказываются сверху и снизу. Хотя этот лист на рисунке кажется плоским, на самом деле он таким не является. Массивная звезда искривляет трехмерное пространство внутри и вокруг звезды, но изобразить это искривление на обычном рисунке (рис. 3.3, слева) невозможно. Это искривление выгибает лист, но на этом рисунке изгиб не виден. Однако мы можем исследовать форму искривления, если будем проводить геометрические измерения в нашем трехмерном пространстве, точно так же, как их делали плос-катики в своей двумерной вселенной. Такие измерения покажут, что существуют прямые, изначально параллельные линии, которые пересекаются в центре звезды, что длина любой окружности вблизи или внутри звезды меньше, чем ее диаметр, умноженный на число п, и что сумма внутренних углов любого треугольника в этой области больше 180°. Все эти свойства искривленного пространства предсказываются шварцшильдовским решением уравнения Эйнштейна.

Чтобы представить наглядно шварцшильдовскую кривизну, мы можем, подобно плоскатикам, мысленно перенести лист из искривленного трехмерного пространства нашей реальной Вселенной в воображаемое плоское гиперпространство (см. справа внизу на рис. 3.3). В этом не искривленном гиперпространстве лист может сохранить свою форму, лишь выгнувшись в том месте, где была звезда. Такие изображения двумерных поверхностей, взятые из нашей искривленной Вселенной и помещенные в гипотетическое плоское трехмерное пространство, и называются вложенными диаграммами.

Не следует поддаваться искушению отождествить третье измерение гиперпространства с третьим пространственным измерением нашей Вселенной. Третье измерение в гиперпространстве не имеет к измерениям нашего пространства никакого отношения. Это измерение, в которое мы не можем перейти и из которого не можем получить никакой информации; оно чисто вымышленное. Зато с его помощью мы сможем наглядно представить геометрию нашего искривленного пространства, пространства, где существуют черные дыры, гравитационные волны, сингулярности и червоточины (см. главы 6, 7, 10, 13 и 14).