Кип Торн - Черные дыры и складки времени. Дерзкое наследие Эйнштейна

Так же, как взгляды на природу пространства и времени оказались совершенно разными, совершенно разной оказалась с их точек зрения, причина сближения траекторий падающих тел. Эйнштейн назвал ее кривизной пространства-времени, Ньютон — приливными силами. Однако поскольку название не меняет сути происходящего, возникновение приливных сил и кривизны пространства-времени должны быть одним и тем же явлением, описанным на разных языках.

Человеку очень трудно представить себе искривленную поверхность, у которой больше двух измерений; наглядно изобразить искривленное четырехмерное пространство-время практически невозможно. Некоторое представление, однако, могут дать двумерные проекции пространства-времени. На рис. 2.6 представлены два примера, показывающие, как кривизна пространства-времени создает приливные растяжение и сжатие, вызывающие океанские приливы и отливы.

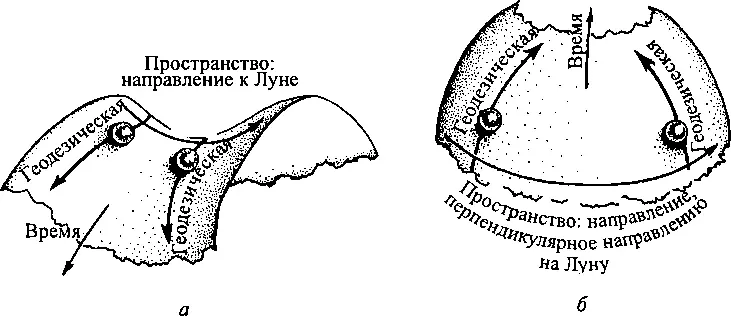
2.6. Два двумерных изображения искривленного пространства-времени вблизи Земли, создаваемого Луной. Это искривление приводит к приливному растяжению вдоль направления к Луне и растяжению поперек него. Эти растяжение и сжатие вызывают океанские приливы (см. Врезку 2.5)

На рис. 2.6 а изображена часть пространства-времени вблизи Земли, включающая время и одну пространственную координату, в качестве которой выбрано направление к Луне. Луна искривляет пространство-время, и эта кривизна растягивает геодезические, как показано на рисунке. Соответственно, наблюдая за двумя свободно движущимися вдоль этих геодезических частицами, мы будем видеть, как они разлетаются, и будем интерпретировать это как результат действия приливных сил. Эти растягивающие силы (кривизна пространства-времени) будут действовать не только на свободно падающие частицы, но и на океаны, создавая выпуклости (см. рис. 2.5) на ближайшей к Луне части поверхности Земли и на противоположной ей. Эти две выпуклости будут пытаться следовать своим геодезическим в пространстве-времени (рис. 2.6а), для чего им следовало бы разлетаться друг от друга, однако земное тяготение (кривизна пространства-времени, создаваемая Землей; на рисунке не показана) препятствует этому, поэтому океаны лишь вздуваются, оставаясь на Земле.

На рис. 2.6 б представлена другая часть пространства-времени вблизи Земли, включающая время и ту пространственную координату, которая перпендикулярна направлению на Луну. Искривление пространства-времени Луной приводит к тому, что геодезические в этом направлении прижимаются друг к другу. Соответственно, мы видим, что свободные частицы, движущиеся по геодезическим перпендикулярно направлению на Луну, сближаются, а океаны на Земле сжимаются в этом направлении. Приливное сжатие приводит к сдавливанию океанов, показанному на Врезке 2.5.

* * *

Эйнштейн был профессором в Праге, когда летом 1912 г., он понял, что приливные силы и кривизна пространства-времени — одна и та же сущность. Это было замечательное открытие, хотя он и не был еще полностью в нем уверен, не представлял его себе в таком законченном виде, как я представляю его вам, и не мог с его помощью полностью объяснить гравитацию. Эйнштейн понял, что кривизна пространства-времени определяет движение свободных частиц, приливы и отливы океанов, но он не понимал еще, как образуется эта кривизна. Ему было ясно, что материя, из которой состоят Солнце, Луна и другие планеты, искривляет пространство-время. Но как она это делает ? Поиск закона искривления стал основной целью Эйнштейна.

Через несколько недель после открытия искривления пространства-времени Эйнштейн переехал из Праги в Цюрих, где он должен был занять место профессора в своей альма-матер, ЕТН. После прибытия в Цюрих в августе 1912 г. Эйнштейн получил совет, который был ему необходим, от своего бывшего сокурсника, Марселя Гроссмана, занимавшего теперь здесь пост профессора математики. Эйнштейн поделился с ним своей идеей о том, что приливные силы есть результат кривизны пространства-времени, и спросил его, существует ли математический аппарат, с помощью которого можно было бы описать такую кривизну и получить законы, по которым материя искривляет пространство-время. Гроссман, который занимался другими проблемами геометрии, сказал вначале, что он не уверен в этом, однако после изучения литературы дал утвердительный ответ: да, нужные уравнения есть. Они были разработаны большей частью немецким математиком Бернхардом Риманом в шестидесятые годы XVII века, итальянцем Георгио Риччи в восьмидесятые и его студентом Туллио Леви-Чивита в девяностые годы того же века. Свой аппарат они называли «абсолютные дифференциальные вычисления» (позднее он получил название «тензорный анализ», а сейчас чаще называется «дифференциальной геометрией»). Однако, сказал Гроссман Эйнштейну, дифференциальная геометрия — ужасно сложная и запутанная вещь, в которую физикам лезть не следует. Увы, другого подхода к описанию законов искривления пространства-времени не было.