Кип Торн - Черные дыры и складки времени. Дерзкое наследие Эйнштейна

Во-вторых, существуют приливные силы, создаваемые Солнцем, которые примерно в два раза слабее лунных и по-другому направлены, поскольку (обычно) Луна и Солнце находятся в разных частях небосвода.

Приливы и отливы, наблюдаемые на Земле, являются результатом комбинации приливных сил, действующих со стороны Луны и со стороны Солнца.

Однако после двенадцати месяцев работы Эйнштейн вынужден был отказаться от этой интересной идеи. Причины были вескими: время относительно, ваше время — это смесь моего времени и моего пространства (если мы движемся друг относительно друга), поэтому, даже если у вас время искривлено, а пространство плоское, у меня будут искривлены и пространство, и время. То же самое можно сказать про все остальные движущиеся системы отсчета. Получается, что ваша, и только ваша система отсчета обладает плоским пространством, соответственно, с точки зрения физических законов, она принципиально отличается от всех остальных систем, а это противоречит принципу относительности.

Тем не менее, Эйнштейн чувствовал, что искривление времени — это ключ к решению проблемы, в таком случае, рассуждал он, предположим, что и время, и пространство искривлены во всех системах отсчета. Может быть, такая комбинированная кривизна объяснит приливные силы?

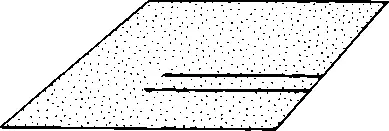
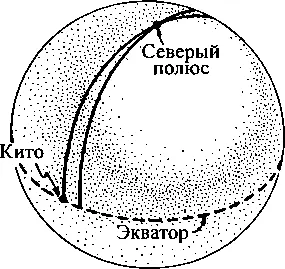
2.4. Две прямые, параллельные изначально, никогда не пересекутся на плоской поверхности, такой, как лист бумаги, нарисованный слева, но могут пересечься на искривленной поверхности, так, как это происходит с меридианами на глобусе (рисунок справа)

Однако такой подход поначалу показался обескураживающим. Во Вселенной может быть бесчисленное множество систем отсчета, движущихся по-разному, и следовательно, надо рассматривать бесконечное количество искривленных времен и пространств! К счастью, Эйнштейн понял, что Герман Минковский дал мощный инструмент, позволяющий существенно упростить ситуацию: «Таким образом, пространство само по себе и время само по себе уходят в тень, и лишь их некоторая комбинация остается независимой реальностью». Существует лишь одно-единственное, уникальное четырехмерное пространство-время в нашей Вселенной; искривления различных пространств и времен должны быть представлены как кривизна единственного, абсолютного пространства-времени Минковского.

Эйнштейн пришел к такому заключению летом 1912 г. После четырех лет насмешек над идеей Минковского он вынужден был принять его абсолютное пространство-время и искривить его!

* * *

Что такое кривизна пространства-времени? Для простоты, рассмотрим сначала искривленную двумерную поверхность. На рис. 2.4 показаны две поверхности: плоская и искривленная. На плоской поверхности (примером которой может быть обычный лист бумаги) проведены две прямые параллельные линии, начинающиеся у одной стороны. Одним из постулатов евклидовой геометрии (названной так в честь создателя — древнегреческого математика Евклида) является то, что параллельные прямые на плоскости никогда не пересекаются. С помощью этого постулата можно проверять, является ли плоской поверхность, на которой нарисованы параллельные прямые: если можно найти хотя бы одну пару изначально параллельных прямых, которые пересекаются где-либо, то данное пространство не является плоским.

В качестве примера искривленного пространства на рис. 2.4 приведено изображение глобуса. Найдем на глобусе город Кито (столицу Эквадора), он расположен на экваторе. Проведем от него прямую линию, направленную на север. Эта линия пройдет по одной и той же долготе к северному полюсу.

Почему эту линию следует считать прямой? Этому есть два различных объяснения. Во-первых, это часть большого круга, и именно вдоль таких линий прокладывают маршруты самолетов, поскольку именно в этом случае они оказываются самыми короткими. Если провести любую другую линию между Кито и северным полюсом на глобусе, она будет длиннее.

Во-вторых, эта линия прямая в смысле рассуждений, которые мы использовали ранее, обсуждая пространство-время: если рассмотреть достаточно маленький участок, через который проходит наша линия, обнаружить на нем кривизну глобуса будет практически невозможно. В пределах этого участка часть большого круга будет прямой в обычном понимании этого слова, такой же, как прямая на плоском листе бумаги. Большой круг на глобусе является прямой линией в пределах любого маленького участка поверхности на своем пути.