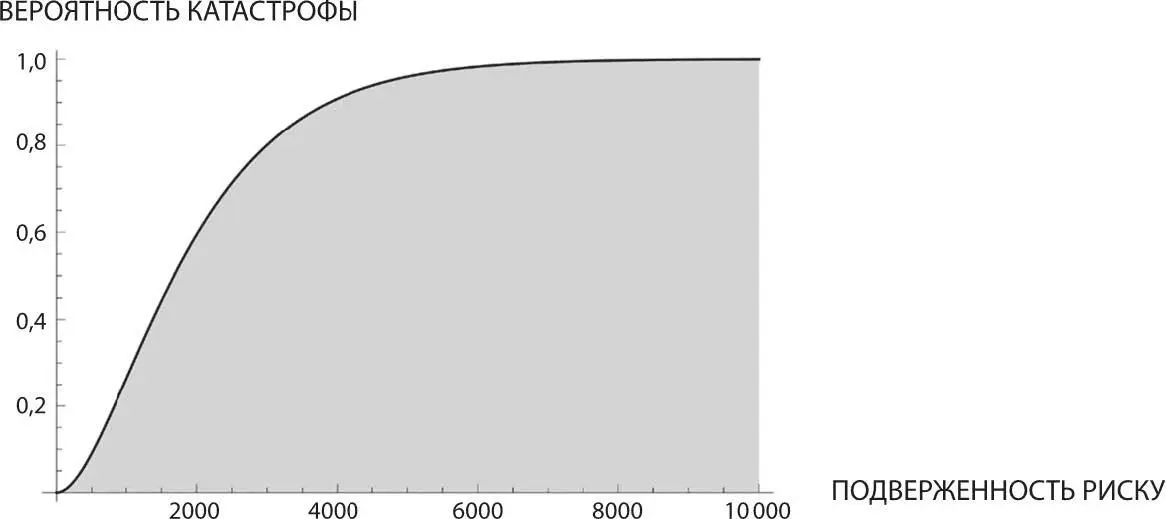
Рис. 9. Почему катастрофа – невозобновляемый ресурс. Сколь бы мала ни была вероятность, со временем то, что неминуемо должно упереться в барьер катастрофы, в него упрется. Никакой риск нельзя воспринимать как «одноразовый»
Мы не должны принимать t → ∞ , не нужна нам и постоянная устойчивость. Мы можем просто увеличить срок жизни. Чем больше t , тем сильнее расходятся операторы ожидания.
Рассмотрим безусловный ожидаемый момент остановки (катастрофы) в дискретной упрощенной модели: 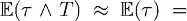
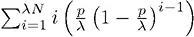 , где λ – количество моментов риска за один период времени, Т – срок оставшейся жизни, р – вероятность катастрофы, последние две величины – за тот же самый период времени, чтобы зафиксировать р . Поскольку
, где λ – количество моментов риска за один период времени, Т – срок оставшейся жизни, р – вероятность катастрофы, последние две величины – за тот же самый период времени, чтобы зафиксировать р . Поскольку 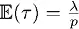 , мы можем калибровать риск при повторении события. Чем больше ожидаемая продолжительность жизни Т (выраженная в периодах времени), тем серьезнее проблема катастрофы. У людей и растений срок жизни короткий, у природы – нет, по крайней мере, для t порядка 10 8 лет; отсюда вероятность ежегодной катастрофы – O (10 –8), а вероятность катастрофы в пределах более короткого промежутка времени – самое большее O (10 –50). Чем выше место в иерархии «индивид – вид – экосистема», тем серьезнее проблема катастрофы. Двойственность базируется на том, что t → ∞ ; поэтому условие не является необходимым для явлений, которые не постоянны, то есть обладают ограниченным сроком жизни.
, мы можем калибровать риск при повторении события. Чем больше ожидаемая продолжительность жизни Т (выраженная в периодах времени), тем серьезнее проблема катастрофы. У людей и растений срок жизни короткий, у природы – нет, по крайней мере, для t порядка 10 8 лет; отсюда вероятность ежегодной катастрофы – O (10 –8), а вероятность катастрофы в пределах более короткого промежутка времени – самое большее O (10 –50). Чем выше место в иерархии «индивид – вид – экосистема», тем серьезнее проблема катастрофы. Двойственность базируется на том, что t → ∞ ; поэтому условие не является необходимым для явлений, которые не постоянны, то есть обладают ограниченным сроком жизни.
Аргумент жирных хвостов. Чем больше допускаемые системой отклонения, тем опаснее проблема катастрофы.
Мы осветим проблему жирных хвостов подробнее. Разумеется, важна дисперсия процесса, однако любые отклонения, которые не выходят за порог катастрофы, значения не имеют.
Логарифмическое преобразование
При аксиоме устойчивости – «риски нужно принимать так, как если бы вы собирались рисковать вечно», применимо только логарифмическое (или аналогичное) преобразование.
Жирнохвостость – свойство, которое обычно вызывает тревогу при отсутствии компактной области определения случайной переменной; жирные хвосты не так опасны, когда переменные ограничены. Однако, как мы видели, достаточно применить логарифмическое преобразование, чтобы случайная переменная с областью определения [0, ∞ ) сменила область определения на (– ∞, ∞ ), после чего к нашему анализу можно применить теорию экстремальных значений. Аналогично: если ущерб определен как положительное число с верхней границей Н , соответствующей катастрофе, возможно изменить область определения с [0, H ] на [0, ∞ ).
Крамер и Лундберг открыли существование трудности в страховом анализе, см. Cramér 1930.
Замечание об эргодичности [125] Спасибо за вопросы Эндрю Лесневски, который помог дать определение тому, что мы имеем в виду под эргодичностью, – значение термина здесь не таково, как в статистической физике.
. Эргодичность нельзя определить статистически, ее нельзя наблюдать, и не существует выявляющего ее теста для временно́го ряда, аналогичного тесту Дики – Фуллера для стационарности (или теста Филлипса – Перрона для порядка интегрирования). Важнее следующее:
Если ваш результат получен путем наблюдения за временны́м рядом, как вы можете говорить о вероятностной мере по ансамблю?
Выход здесь тот же, что и в случае арбитражной схемы: статистического теста нет, но, и это главное, есть вероятностная мера, определяемая предположительно (аргумент «бесплатных булочек не бывает»). Далее, рассмотрите аргумент стратегии «самофинансирования» через, например, динамическое хеджирование. В пределе мы допускаем, что закон больших чисел уменьшит отдачу и мы никогда не дойдем до убытков и до поглощающего барьера. Такая ситуация удовлетворяет нашему критерию эргодичности, однако определить ее статистически невозможно. Более того, почти вся литература о межвременных инвестициях / потреблении требует, чтобы вероятность катастрофы была нулевой.
Мы не утверждаем, что данный безопасный или случайный процесс эргодичен; мы утверждаем, что, учитывая вероятность по ансамблю (полученную перекрестными методами, допущенную через субъективные вероятности или просто обусловленную аргументами арбитража), стратегия принятия риска должна обладать подобными свойствами. Эргодичностью обладает функция случайной переменной или процесса, но не сам процесс. И эта функция не должна допускать катастрофы.
Читать дальше
Конец ознакомительного отрывка
Купить книгу


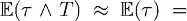
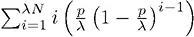 , где λ – количество моментов риска за один период времени, Т – срок оставшейся жизни, р – вероятность катастрофы, последние две величины – за тот же самый период времени, чтобы зафиксировать р . Поскольку
, где λ – количество моментов риска за один период времени, Т – срок оставшейся жизни, р – вероятность катастрофы, последние две величины – за тот же самый период времени, чтобы зафиксировать р . Поскольку 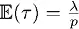 , мы можем калибровать риск при повторении события. Чем больше ожидаемая продолжительность жизни Т (выраженная в периодах времени), тем серьезнее проблема катастрофы. У людей и растений срок жизни короткий, у природы – нет, по крайней мере, для t порядка 10 8 лет; отсюда вероятность ежегодной катастрофы – O (10 –8), а вероятность катастрофы в пределах более короткого промежутка времени – самое большее O (10 –50). Чем выше место в иерархии «индивид – вид – экосистема», тем серьезнее проблема катастрофы. Двойственность базируется на том, что t → ∞ ; поэтому условие не является необходимым для явлений, которые не постоянны, то есть обладают ограниченным сроком жизни.
, мы можем калибровать риск при повторении события. Чем больше ожидаемая продолжительность жизни Т (выраженная в периодах времени), тем серьезнее проблема катастрофы. У людей и растений срок жизни короткий, у природы – нет, по крайней мере, для t порядка 10 8 лет; отсюда вероятность ежегодной катастрофы – O (10 –8), а вероятность катастрофы в пределах более короткого промежутка времени – самое большее O (10 –50). Чем выше место в иерархии «индивид – вид – экосистема», тем серьезнее проблема катастрофы. Двойственность базируется на том, что t → ∞ ; поэтому условие не является необходимым для явлений, которые не постоянны, то есть обладают ограниченным сроком жизни.










