Сергей Труфанов - Наука логики Гегеля в доступном изложении

Умозаключения рефлексии

§ 190. Умозаключения рефлексии по своему объективно-логическому значению соответствуют второй фигуре: В – Е – О, где серединой являются единичности . Единичности различаются между собой по своим свойствам. Одни студенты получают фундаментальное образование, другие –медицинское, третьи – техническое. По этим параметрам они отличаются друг от друга и по ним же они обособляются в конкретные всеобщности, имеющие уже вполне объективное существование ( классический университет, политехнический институт, медицинский институт).

а) Когда ряд единичных субъектов обладает каким-то одним особенным свойством, тогда мы имеем умозаключение совокупности ( общности ). Его форма: Е – О – В или, наоборот, В – О – Е. (Местоположение крайних членов, как мы уже говорили, роли не играет.) Например: Иванов получает фундаментальное образование . – Все те, кто получает фундаментальное образование, являются студентами классического университета. – Следовательно, Иванов – студент классического университета.

Умозаключение совокупности имеет следующий недостаток: всё то, что утверждается в его выводе, уже содержится в его большой посылке. ( Все те, кто получает фундаментальное образование являются студентами классического университета . Все те, кто получают медицинское образование, являются студентами мединститута ). Но чтобы утверждать, что какое-то определённое свойство присуще всем , этому надо прежде получить подтверждение. Поэтому умозаключение совокупности с необходимостью отсылает нас к умозаключению индукции .

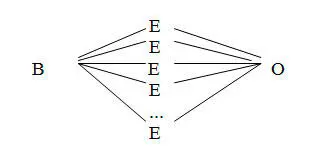
б) Форма у мозаключения индукции : В – Е – О. Это умозаключение приводит мысль от констатации единичных случаев к утверждению общего вывода. Пример: Иванов – студент классического университета, Петров – студент классического университета, Сидоров – студент классического университета, ... и т.д. – Иванов получает фундаментальное образование, Петров получает фундаментальное образование, Сидоров получает фундаментальное образование, ... и т.д. – Следовательно, все студенты классического университета получают фундаментальное образование.

Фигура индуктивного умозаключения имеет следующий вид:

Однако единичные примеры в индуктивном умозаключении никогда не могут быть исчерпаны полностью, поэтому индукция приводит мышление к умозаключению третьей формы – аналогии , которая дополняет умозаключение индукции и компенсирует его неполноту.

в) У мозаключение аналогии (сходства). Его форма: О – В – Е, где опосредствующей серединой является всеобщее . Рассуждая по аналогии, мы основываемся на том, что все известные нам вещи одного порядка обладают некоторым свойством. Из этого мы делаем вывод, что и все другие вещи того же порядка обладают таким же свойством. Пример: Все студенты классического университета получают фундаментальное образование – Иванов является студентом классического университета – Следовательно, Иванов также получает фундаментальное образование .

Вывод из умозаключения аналогии оказывается тождественным первой посылке первого умозаключения рефлексии – умозаключения совокупности . В результате мы вновь получили сомкнувшийся круг умозаключений. Но при этом всеобщность изменила свой характер. В умозаключении совокупности мы имели всеобщность как простую полноту охвата единичных субъектов в её отличии от их других всеобщностей. Теперь же, в умозаключении аналогии , всеобщность приобрела характер объективной всеобщности. Говоря другими словами, первоначально абстрактная целокупность студентов классического университета, в её простом отличии от целокупности студентов других вузов, становится теперь целокупностью действительного классического университета из какого-нибудь города N-ска. Ну а поскольку действительный университет представляет собой уже не абстрактную, а реально существующую всеобщность, причём существующую в качестве самой себя как всеобщности, постольку теперь именно эта объективная всеобщность становится средним членом умозаключения, связующим особенное и единичное, как свои подчинённые моменты. Благодаря этому мышление переходит на ступень умозаключений необходимости.