Ник Антилл - Оценка компаний - Анализ и прогнозирование с использованием отчетности по МСФО

Бета определяется как ковариация с рынком. Акции, ковариация которых с рынком выше средней, характеризуются высоким коэффициентом бета, акции, ковариация которых с рынком ниже средней, характеризуются низкой бетой. САРМ не подразумевает, что только рыночные колебания влияют на курсы акций. На самом деле САРМ предполагает, что цены акций меняются под влиянием рынка, а также специфических для каждой компании факторов. Но риск каждой акции в качестве составляющей инвестиционного портфеля определяется только влиянием рынка. Данное рассуждение проиллюстрировано на рис. 2.7.

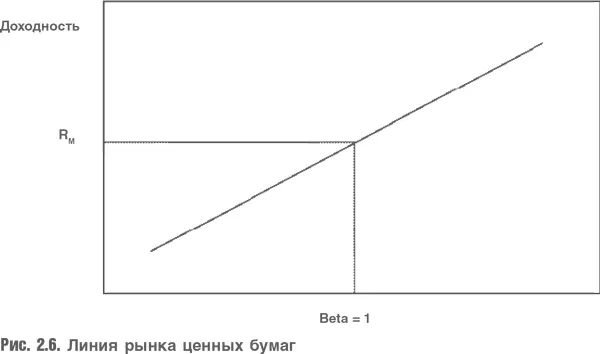
Примером компаний, акции которых имеют высокую бету, могут быть компании наиболее волатильных секторов экономики, например жилищного строительства, или наиболее чувствительных к колебаниям рынка ценных бумаг, например компаний страхования жизни. Примерами акций с низкой бетой могут быть акции компаний коммунального обслуживания или розничные сети по торговле продовольствием. Ниже будет подробнее освещена способность компаний повышать или понижать бету путем изменения доли заимствований в финансировании.

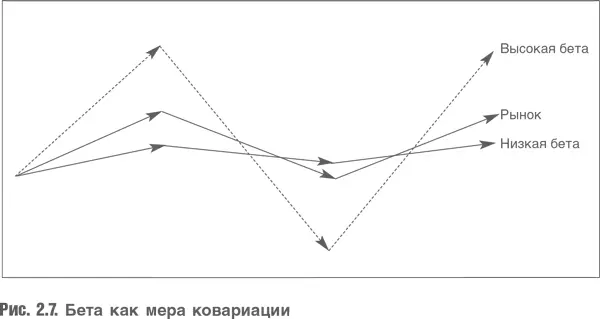
Обычно коэффициент бета вычисляется с помощью парной регрессии доходности актива за некоторую последовательность периодов к доходности рынка в целом за ту же последовательность периодов. На рис. 2.8 представлено множество наблюдений доходности акции относительно доходности рынка за ряд периодов; на практике часто берутся помесячные показатели доходности за три или пять лет. Историческое значение бета акции определяется как наклон линии регрессии. Безусловно, при таком подходе возникают проблемы статистического характера. Акции отдельных компаний часто слабо коррелируют с рынком. Теория оперирует ожидаемыми значениями беты, а не историческими. На практике бета обычно рассчитывается с использованием баз данных (например, Bloomberg, DataStream или др.).

Существуют проблемы, связанные со стандартным подходом к расчету беты. Первая: такие расчеты базируются на исторических данных, а ставка дисконта определяется с учетом ожидаемой беты (на соответствующий период). Вторая: многие расчеты оказываются статистически незначимыми. Третья: за какой период должна измеряться бета?

Вернемся к рис. 2.5. При его построении предполагается, что доходность рыночного портфеля выше доходности безрискового актива. Это, безусловно, разумно. Хотя инвесторы способны путем диверсификации исключить все специфические риски отдельных акций, они не могут исключить рыночный риск – диверсифицировать его невозможно. Поэтому инвесторы, готовые нести рыночный риск, должны получать компенсацию в виде дополнительной доходности. Зная цену рыночного риска, можно начертить линию рынка капитала и использовать ее для вычисления требуемой доходности для каждой отдельной акции. Но как рассчитать размер рыночной премии за риск?

Как и в случае с коэффициентом бета, один из способов – обратиться к истории. В различных базах данных (в Англии исследования «Акции – государственные ценные бумаги» и более современные исследования Лондонской школы бизнеса, в США исследования компании Ibbotson) ежегодно приводятся показатели доходности разных классов ценных бумаг. При этом возникает методический вопрос: должен каждый год рассматриваться как самостоятельная единица и годовая доходность при этом арифметически усредняться или следует весь рассматриваемый период (несколько десятилетий) рассматривать как одну единицу и годовую доходность рассчитывать как среднее геометрическое? Второй вариант представляется более предпочтительным, но и здесь, как в случае с коэффициентом бета, важно, соответствуют ли основанные на исторических данных оценки ожидаемым в будущем параметрам?

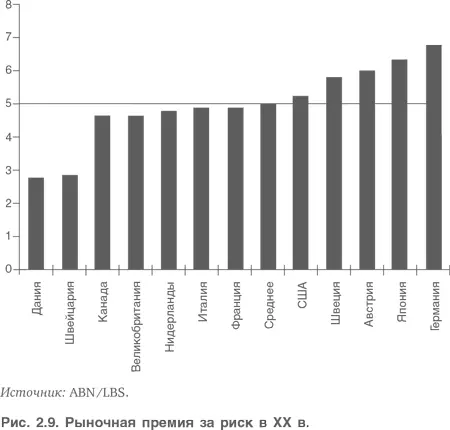
На рис. 2.9 приведены основанные на исторических данных за ХХ в. оценки разницы между значениями годовой доходности акций и долгосрочных государственных облигаций на рынках разных стран. Среднее арифметическое таких разниц составляет около 5 %, т. е. в среднем акции сулят примерно на 5 % бóльшую доходность, чем долговременные государственные облигации за этот период.