Андрей Гуслистый - Управление инвестициями. Диверсификация портфеля, риск и слежение за рынком

Прежде чем узнать, какая из последовательностей является реальной последовательностью, вы, возможно, не удивитесь, если узнаете, что ответ «b» выбирает подавляющее большинство людей, которым задают этот вопрос. Их довод: «b» выглядит как реальная последовательность. Давайте исследуем популярный ответ, используя подбрасывание монеты, чтобы рассмотреть понятие случайности, или статистической независимости.

Предположим, что вы поставили 1 доллар на орла при однократном подбрасывании монеты. Это пари с равными шансами; орел и решка одинаково вероятны. Приблизительно в половине случаев вы выиграете 1 доллар; в половине случаев вы проиграете 1 доллар. Теперь предположим, что у вас два раза подряд выпал орел. Каковы шансы на то, что в следующем пари у вас выпадет орел? Они все еще 50–50?

Игроки интуитивно знают, что серия из трех орлов подряд выпадает не часто. Это верно. Точно так же игроки в рулетку знают, что три раза подряд «черное» выпадает не часто. Но изменяют ли эти серии шансы на выигрыш следующего броска монеты или следующего вращения рулетки? Как игрок мог бы использовать это знание для следующего пари? Надлежащее использование таких знаний – и, что более важно, то, как возникают подобные решения при отборе инвестиций – приходит от понимания того, что является, а что не является предсказуемым в случайных событиях.

Случайное (или статистически независимое) событие – происшествие, результат которого не может быть предсказан на основе предыдущих событий. Примеры случайных событий – результат подбрасывания монеты и вращения рулетки. Для таких событий результат каждой отдельной попытки определяется случаем, и его невозможно предсказать. Например, если вы бросаете симметричную монету, невозможно знать заранее, упадет ли эта конкретная монета орлом или решкой вверх.

Давайте вернемся к вопросу шансов игрока после рассмотрения серии (последовательности результатов одного вида). Игроки часто изобретают схемы пари, основанные на «инверсиях» или «сериях». После наблюдения последовательности с одним результатом – скажем, трех последовательных бросков монеты, упавшей орлом вверх, или трех последовательных вращений рулетки, при которых выпадает черное – они принимают особую стратегию заключения пари. Некоторые игроки делают вывод, что нехорошо ожидать еще одного орла после того, как два орла уже выпало. Они рассуждают, что, в конце концов, все знают, что три орла подряд – относительно редкое событие. Таким образом, они делают вывод, что орлы уже «израсходованы». Наоборот, другие игроки рассуждают, что игра «набирает обороты» и что вероятность выпадения орла при следующем броске выше обычного. Предполагая, что монета или рулетка являются правильными и симметричными, обе игровые системы бесполезны!

Тщетность систем «пришло время для перемены» и «игра набирает обороты» станет понятной, если вы проанализируете игру в подбрасывание монеты. Каждый бросок имеет два возможных результата: орел или решка. Когда выпадает орел, решка не может выпасть, и наоборот. Вероятность, или возможность, того, что симметричная монета будет падать орлом вверх, равна половине. Это означает, что, в конечном счете, вы ожидаете, что половина результатов будет орлами.

Вы должны помнить два момента:

1. Невозможно предсказать, какой результат будет при любом определенном броске.

2. После многих повторений, приблизительно половина результатов будет орлами, а половина – решками.

Рассмотрите четыре возможных результата двух последовательных подбрасываний монеты. Они обозначены следующим образом:

ОО, ОР, РО, РР

Здесь ОО означает, что монета приземлилась орлом при первом броске и также орлом при втором броске; ОР означает орла, за которым следовала решка; и так далее. Для двух последовательных бросков невозможны никакие другие комбинации орла и решки. Эта ситуация показана в Табл. 2.

Табл. 2 Четыре возможных результата двукратного подбрасывания монеты

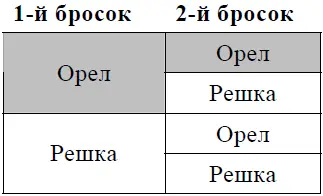
Возникновение двух орлов подряд показано в заштрихованной области. Двойное выпадение орла – один из четырех возможных результатов. Теперь предположите, что, после того как выпало два орла, ваш друг говорит: «Держу пари, что у тебя не может выпасть еще один орел». Каковы ваши шансы?

В азартных играх типа рулетки, игры в кости или бросания монеты последовательные ходы называют независимыми событиями. Колесо рулетки, кости или монеты не имеют памяти. После двух бросков монета «не помнит», какая из четырех возможных последовательностей, показанных в Табл. 2, имела место. Ничто из того, что было раньше, не может повлиять на монету. Остается 50-процентный шанс того, что при следующем броске выпадет орел, и 50-процентный шанс того, что это будет решка. После двух орлов подряд вероятность того, что монета приземлится орлом вверх ничуть не больше и не меньше, чем она была при предыдущих бросках – это все еще пари с равными шансами. Знание того, что произошло в прошлом, бесполезно в предсказании следующего события.