Вадим Цудикман - Опционы - Разработка, оптимизация и тестирование торговых стратегий

Подразумеваемая волатильность.Показатель волатильности, рассчитанный не на базе исторических цен базового актива (см. историческая волатильность), а выведенный из текущих рыночных цен опционов. Модели ценообразования используют прогнозное значение волатильности для расчета теоретической (справедливой) стоимости опционов. В качестве него в формулу для вычисления цены опциона можно подставить значение исторической волатильности. Если в модельную формулу подставить рыночную цену опциона (считая ее справедливой) и решать обратную задачу, то можно вычислить волатильность, «подразумеваемую» данной стоимостью опциона. Подразумеваемая волатильность выражает ожидания рынкаотносительно будущей изменчивости цен базового актива. Кроме того, этот показатель является общепризнанным мерилом дороговизны опционов. Зачастую расхождения в величинах подразумеваемой и исторической волатильности создают благоприятные возможности для реализации многих опционных стратегий.

Премия.Стоимость опциона, уплачиваемая продавцу покупателем. На рынке опционов на акции премия обычно котируется из расчета на одну акцию, в реальности же стандартный контракт состоит, как правило, из опционов на 100 акций.

Ро.Частная производная первого порядка стоимости опциона по безрисковой процентной ставке (величина, на которую изменяется стоимость опциона при изменении процентной ставки на 1 пункт). Ро выражает чувствительность стоимости опциона к изменениям процентной ставки.

Тета. Частная производная первого порядка стоимости опциона по времени (величина, на которую изменяется стоимость опциона при уменьшениивремени оставшегося до истечения на единицу времени). Тета выражает скорость временного распада .

Цена исполнения (страйк).Зафиксированная в контракте цена, по которой покупатель опциона может реализовать свое право купить или продать базовый актив.

На рис. П1 схематично представлены платежные функции отдельных опционов колл и пут для покупателя (длинные опционы)и продавца (короткие опционы). Сплошными линиями показаны платежные функции на дату исполнения, прерывистыми линиями – на некоторою промежуточную дату, предшествующую дате исполнения. При заданной цене базового актива позиция покупателя опциона тем больше, чем больше времени остается до истечения (прерывистые линии на рисунках расположены выше сплошных линий). И наоборот, чем ближе дата истечения, тем дороже позиция продавца опциона (прерывистые линии на рисунках расположены ниже сплошных линий). Это объясняется тем, что в стоимости опциона присутствует как внутренняя стоимость, так и временная стоимость. Последняя непрерывно уменьшается по мере приближения даты истечения (это явление называется временным распадом).

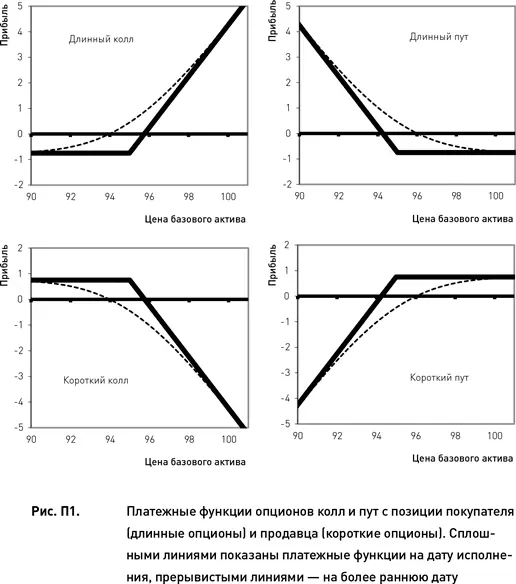
Из рис. П1 следует, что покупатель опциона колл получает теоретически неограниченную прибыль при росте цены базового актива и ограниченный убыток в случае ее падения (максимальный убыток ограничен величиной премии, уплаченной при покупке опциона). Покупатель опциона пут получает теоретически неограниченную прибыль при падении цены базового актива и ограниченный убыток в случае ее роста. В обоих случаях максимальный убыток ограничен величиной премии, уплаченной при покупке опциона.

Платежные функции коротких опционов являются зеркальным отражением платежных функций длинных опционов (рис. П1). Прибыли продавцов опционов лимитированы размером получаемой премии, а их убытки теоретически безграничны и зависят от силы ценового движения базового актива. Чем больше вырастет цена базового актива, тем большим будет убыток коротких коллов. Соответственно, чем больше цена снизится, тем большим будет убыток коротких путов.

Комбинируя разные опционы, можно получить более сложные формы платежных функций. Это является одним из важнейших преимуществ опционов – они дают возможность строить множество разнообразных нелинейных профилей прибыли, что существенно расширяет возможности инвестора.

Используя определенные принципы сочетания опционов (соотношение длинных и коротких позиций, соотношение колов и путов, взаиморасположение и соотношения страйков и дат истечения), можно создавать комбинации, обладающие характерными видами платежных функций. Принято классифицировать комбинации в зависимости от принципа их построения и вида свойственных им платежных функций. Приведем несколько примеров наиболее популярных стратегий.