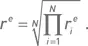При определении элементарного периода времени существенным фактором является то, что итог многих сделок, связанных с опционами может быть определен только на момент их экспирации. Многие опционные стратегии основываются на выборе торговых вариантов с помощью критериев, оценивающих опционы в момент их покупки или продажи, ориентируясь на дату экспирации. Это связано не только с удобством применения математического аппарата ценообразования опционов, но и большей определенностью цен опционов в момент экспирации. Традиционным временем экспирации опционов на CBOE (основной опционной биржи) является третья пятница каждого месяца. Поэтому для стратегий, торгующих на рынке опционов на акции, возникает естественная месячная периодичность измерений прибыльности, связанная со стандартным временем экспирации. Для таких стратегий элементарный период времени составляет один месяц.
Для стратегий, работающих с опционами далеких серий, момент экспирации уже не будет играть такую ключевую роль, как для опционов ближайших серий. В этом случае возрастает роль других временных ориентиров, использование которых более обоснованно для промежуточных оценок текущего портфеля. В последнее время вводятся биржами и получают растущую популярность опционы с недельной периодичностью экспираций. Для стратегий, работающих с ними, удобным будет недельный элементарный период времени.
Стратегии с применением техник динамического хеджирования могут сопровождаться большой интенсивностью сделок с ликвидным базовым активом и редкими сделками по опционам. В таких стратегиях с большой частотой сделок и моментов принятия решений удобным временем оценки показателей стратегии могут быть дневные (и даже более дробные) периоды времени.
5.5.2. Обзор показателей прибыльности стратегии
Предположим, что требуется оценить эффективность стратегии на интервале времени τ = [ T 0, T N ] с последовательностью промежуточных моментов времени ( T 0, T 1 …, T N ). Для простоты будем измерять время в днях. Тогда длина интервала τ составит T N – T 0 дней или в годах примерно Δ T = ( T N – T 0 )/ A , где A = 365,25 календарных дней. Обозначим через ( E 0, E 1 …, E N ) последовательность значений величины капитала, который оценивается в каждый из моментов времени ( T 0, T 1 …, T N ) по заложенному в систему бэктестинга алгоритму. Обычно для оценки капитала используется ликвидационная стоимость всех позиций стратегии, рассчитанная по ценам закрытия соответствующего дня, включая свободные денежные средства. Итоговый доход стратегии составит величину Δ E = E N – E 0 .
Будем рассматривать два вида доходности, соответствующих двум подходам к управлению капиталом (имеется ввиду первый уровень системы управления капиталом, см. главу 4), – с постоянной суммой, инвестируемой в стратегию в каждый период времени, и с реинвестицией.
Первый подход удобен для анализа среднего результата серии однотипных портфелей. Этот случай хорошо подходит для стратегии, основанной на продаже волатильности незадолго до экспирации, когда каждая экспирации порождает один отдельный портфель. При этом для каждого элементарного периода времени используется одна и та же сумма E 0 . Для случая управления капиталом с постоянной суммой инвестиций будем пользоваться линейной годовой доходностью:
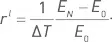
Эта величина соответствует средней арифметической доходности указанной серии, приведенной к годовому масштабу.
Второй подход к управлению капиталом более удобен для сравнения результатов стратегии с эталонным доходом типа непрерывно начисляемой процентной ставки (например, безрискового актива) или с определенным индексом (например, S&P 500). В таком случае следует пользоваться экспоненциальной годовой доходностью:
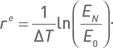
Экспоненциальная доходность соответствует средней геометрической доходности, приведенной к годовому масштабу.
Моменты времени, когда производятся измерения капитала, будем связывать с моментами экспирации опционов. В этом случае мы приходим к серии месячных прибылей и убытков. Пусть N – число месяцев в периоде, на котором производится бэктестинг стратегии. В линейном случае предполагается, что стартовый капитал каждого месяца равен E i−1 , а инвестируемый капитал всегда равен E 0 . Тогда прибыль i -го месяца p l i = E i − E i−1 , средняя прибыль за месяц 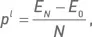 средняя доходность
средняя доходность 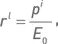 доходность i -го месяца
доходность i -го месяца 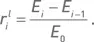 В экспоненциальном случае стартовый и инвестируемый капиталы для каждого месяца совпадают с конечным капиталом предыдущего месяца. О средней месячной прибыли говорить не имеет смысла, поскольку в каждом месяце инвестируется разная сумма. Доходность i -го месяца
В экспоненциальном случае стартовый и инвестируемый капиталы для каждого месяца совпадают с конечным капиталом предыдущего месяца. О средней месячной прибыли говорить не имеет смысла, поскольку в каждом месяце инвестируется разная сумма. Доходность i -го месяца 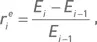 в качестве средней доходности экспоненциального случая разумно принимать среднюю геометрическую доходность
в качестве средней доходности экспоненциального случая разумно принимать среднюю геометрическую доходность 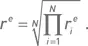
Читать дальше
Конец ознакомительного отрывка
Купить книгу

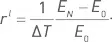
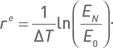
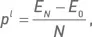 средняя доходность
средняя доходность 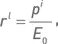 доходность i -го месяца
доходность i -го месяца 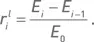 В экспоненциальном случае стартовый и инвестируемый капиталы для каждого месяца совпадают с конечным капиталом предыдущего месяца. О средней месячной прибыли говорить не имеет смысла, поскольку в каждом месяце инвестируется разная сумма. Доходность i -го месяца
В экспоненциальном случае стартовый и инвестируемый капиталы для каждого месяца совпадают с конечным капиталом предыдущего месяца. О средней месячной прибыли говорить не имеет смысла, поскольку в каждом месяце инвестируется разная сумма. Доходность i -го месяца 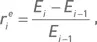 в качестве средней доходности экспоненциального случая разумно принимать среднюю геометрическую доходность
в качестве средней доходности экспоненциального случая разумно принимать среднюю геометрическую доходность