Вячеслав Демидов - Как мы видим то, что видим [издание 3-е , перераб. и доп.]

Ну а насчет зрения – голографический подход объясняет немало. Например, возникновение иллюзий, с чем иные модели зрительной системы плохо справляются.

Вадим Давыдович порылся в бумагах на столе и вытащил фотографию. На ней виднелись светлые пятна на темном фоне.

– Вот это голографическая интерпретация иллюзии Мюллера – Лиера...

Несмотря на мудреное название, иллюзия знакома всем, это линии с «хвостиками»: длина линий одинакова, но «хвостики» направлены у одной наружу, а у другой внутрь, так что в итоге линии кажутся разной длины. Долгое время считали, что глаз ошибается в размерах потому, что скользит от одного края картинки до другого. И если «хвостики» направлены в ту же сторону, что движение, взор «протягивается» по ним, психологически удлиняя размер. Наоборот, встречая противодействующие «хвостики», взор тормозится – линия кажется короче. Эту версию опроверг голографический эксперимент, а перед тем – психологический.

Рис. 48.Четыре голограммы (слева) и то, что они показывают (справа). В кружке иллюзия Мюллера-Лиера

Для психологического эксперимента изображение делали неподвижным относительно глаза: помещали диапозитив в миниатюрную присоску Ярбуса на глазном яблоке. Теперь водить зрачком по линиям возможности нет, а испытуемые все равно видят их иллюзорно разной длины.

Стало ясно, что рождается иллюзия не в глазу как таковом, а гораздо глубже: на уровне коры.

Голографический эксперимент заключался в том, что картинку с иллюзией Мюллера – Лиера превращали в голограмму, а потом выбрасывали из нее высокочастотные члены разложения Фурье. После этого восстановленное (и несколько менее четкое, естественно) изображение было именно таким, каким оно кажется: иллюзорно большая линия выглядит на голограмме действительно более длинной, нежели та, у которой «хвостики» вовнутрь.

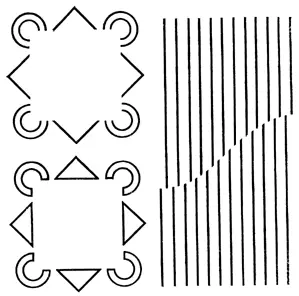
Точно так же был вскрыт голографический механизм иллюзии «птичек» – разбросанных по листу бумаги равносторонних треугольников (они слева вверху на этой картинке).

Рис. 49.Голографический механизм иллюзии «птичек»

«Птички» летят, когда на них смотришь, то в одну сторону, то в другую, то в третью... Причина их своенравного поведения в том, что зрительный аппарат каждый раз использует не весь «мозговой фильтр Фурье», а только какую-то его часть.

Этот эффект великолепно демонстрирует ЭВМ: она показывает на экране телевизора «полет птичек» в любом направлении (нижний ряд). Для этого компьютер смотрит на треугольнички через Фурье-фильтр (справа вверху), соответственно синтезированный компьютером, но выбирает то одну часть фильтра, то другую, то третью (см. второй ряд изображений на рисунке справа).

А какой биологический, природный смысл был формировать такую сверхсложную опознающую мозговую систему, как Фурье-анализатор и кусочная квазиголография? Огромный.

Рис. 50.Слева вверху – светлый квадрат, которого нет на самом деле. Справа – линия, которой также нет на самом деле. Причина? Голографическое устройство зрительного аппарата, обеспечивающее анализ текстур

Помните, рассматривая «обманы зрения», мы много говорили о текстурах? А теперь посмотрите вокруг: мир – это мозаика текстур. Но что такое эти текстуры, как не естественные, природой изготовленные решетки?

Все огромное многообразие природных текстур может быть представлено в затылочной коре соответствующим многообразием кодов – ансамблей ответов каждого модуля (паттернов, как для краткости называют такой ансамбль). То есть мозг получает сведения, насколько дробны и упорядочены элементы текстур, насколько и в каком направлении наклонены. Любая картинка оказывается представленной в затылочной коре некоторой мозаикой паттернов – соответственно множеству полей нейронов и множеству модулей коры.

Для каждой картинки, для каждого предмета мозаика оказывается особой. То есть получается мозаика признаков, позволяющих отличать предмет от предмета, пейзаж от пейзажа, лицо от лица...

– Мы назвали эти признаки простыми, – сказал Глезер. – С их помощью можно описать и запомнить любую картинку, от чрезвычайно пестрой до контурной, ведь гладкую поверхность можно рассматривать как выродившуюся «до нуля» текстуру. А математически это означает, что совокупность сигналов модулей выглядит многомерным пространством, и каждое конкретное изображение есть точка в нем.