Константин Александрович Бакшт - Вкус жизни. Как достигать успеха, финансовой свободы и управлять своей судьбой

Очень наглядно иллюстрирует действие магии сложного процента так называемое «Правило 72». Чтобы быстро приблизительно представить, сколько лет потребуется для удвоения стоимости Вашей инвестиции, просто разделите 72 на норму прибыли: доходность в 4 % дает 18 лет; в 6% – 12 лет; в 10% — 7 с небольшим лет и т. д.

«Правило 72» полезно для инвесторов, откладывающих деньги сегодня, чтобы получить доход завтра в еще одном варианте. При любой заданной норме прибыли «Правило 72» показывает, на протяжении скольких лет Вам придется регулярно инвестировать какую-то сумму, прежде чем Вы сможете остановиться, чтобы приступить к изъятию той же самой суммы, не истощая своего капитала.

Расчет «Правило 72»

Тем, кто впервые знакомится с «Правилом 72», сначала бывает сложно понять всю его важность. Умом сразу схватить его суть в полной мере не так уж просто. А здравый смысл в данном случае (как и при анализе рисков) скорее вводит нас в заблуждение, чем помогает. Однако остается одно надежное средство, позволяющее разобраться с тем, как работает «Правило 72». Давайте все посчитаем!

Использование «Правила 72»: рост капитала размещенного под сложный процент

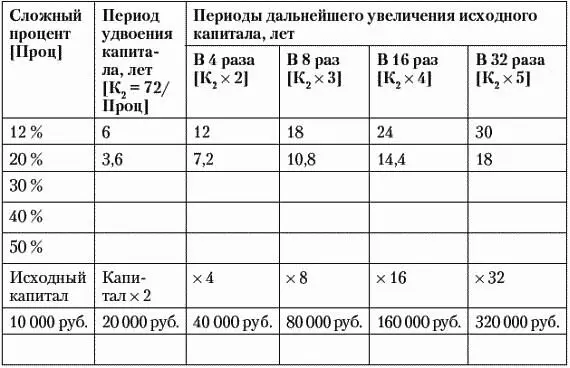
В приведенной выше таблице часть расчетов уже выполнена. А другую часть мы сможем сделать вместе, чтобы набить руку в финансовых вычислениях. Вообще, если Вы планируете серьезно заниматься управлением личными финансами и инвестициями, то подобные финансовые расчеты будете делать часто и в большом количестве.

Первая строка расчета: предположим, Ваш капитал размещен под 12% годовых. Каков в этом случае будет период удвоения капитала? 72 разделить на 12 будет 6 лет.

Если через 6 лет не изымать ни исходного капитала, ни процентов (которые мы добавляем к исходному капиталу), то еще через 6 лет капитал опять удвоится. Значит, тот капитал, с которого мы начинали процесс инвестиций, за 6 + 6 = 12 лет увеличится в 2 × 2 = 4 раза. Таким образом, капитал растет в геометрической прогрессии.

Если после 12 лет инвестиций по-прежнему не изымать капитал и по-прежнему добавлять проценты к основному капиталу, еще через 6 лет капитал снова удвоится. То есть за 6 + 6 + 6 = 18 лет с начала инвестиций капитал увеличится в 2 × 2 × 2 = 8 раз. Аналогично: за 6 + 6 + 6 + 6 = 24 года с начала инвестиций капитал увеличится в 2 × 2 × 2 × 2 = 16 раз. За 6 + 6 + 6 + 6 + 6 = 30 лет с начала инвестиций капитал увеличится в 2 × 2 × 2 × 2 × 2 = 32 раза.

Если бы мы в самом начале инвестировали 10 000 рублей, то спустя 6 лет они превратились бы в 20 000 рублей. Еще через 6 лет, то есть через 12 лет с момента начала инвестиций, – в 40 000 рублей. Через 18 лет с момента начала инвестиций 10 000 рублей превращаются в 80 000 рублей. Через 24 года – в 160 000 рублей. А через 30 лет – в 320 000 рублей. Как видите, чем больше проходит времени, тем быстрее идет процесс увеличения капитала.

А что будет, если доходность на капитал, инвестированный под сложный процент, составит 20% годовых? В этом случае период удвоения капитала [К2] составит 72 / 20 = 3,6 года.

В соответствии с расположенной выше таблицей мы можем сразу рассчитать следующие периоды удвоения капитала. Исходный капитал вырастет в 4 раза через [К2] × 2 = 3,6 × 2 = 7,2 года с начала инвестиций. Аналогично:

☼ исходный капитал вырастет в 8 раз через [К2] × 3 = 3,6 × 3 = 10,8 года с начала инвестиций;

☼ исходный капитал вырастет в 16 раз через [К2] × 4 = 3,6 × 4 = 14,4 года с начала инвестиций;

☼ исходный капитал вырастет в 32 раза через [К2] × 5 = 3,6 × 5 = 18 лет с начала инвестиций.

То есть при доходности 20% годовых инвестированные под сложный процент 10 000 рублей превратятся в 160 000 рублей уже через 14,4 года, а в 320 000 – через 18 лет.

Но и это не предел. В 2010 году, равно как и в предыдущие 15 лет, в России есть немало вариантов инвестиций с доходностью 30–40% годовых. Давайте посмотрим, что происходит с исходным капиталом при такой доходности.

Если Вы инвестируете капитал под сложный процент при 30% годовых, то период удвоения капитала [К2] составит 72 / 30 = 2,4 года. Заполняем дальше всю строку таблицы по аналогии с предыдущей строкой.

☼ Исходный капитал вырастет в 4 раза через [К2] × 2 = 2,4 × 2 = 4,8 года с начала инвестиций.

☼ Исходный капитал вырастет в 8 раз через [К2] × 3 = 2,4 × 3 = 7,2 года с начала инвестиций.

☼ Исходный капитал вырастет в 16 раз через [К2] × 4 = 2,4 × 4 = 9,6 года с начала инвестиций.

☼ Исходный капитал вырастет в 32 раза через [К2] × 5 = 2,4 × 5 = 12 лет с начала инвестиций.