Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

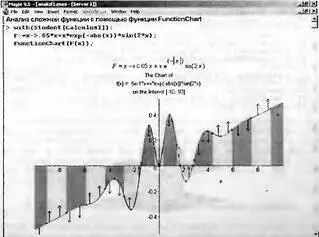
Рис. 8.73. Анализ и визуализация сложной функции, заданной функцией пользователя

Рисунок 8.73 дает наглядное представление о поведении заданной функции. Рекомендуется опробовать данную процедуру на других функциях. Следует отметить, что, поскольку процедура использует функции minimize и maximize, она может давать сбои при исследовании сложных функций, содержащих специальные математические функции или особенности. Данная процедура дает хорошие результаты при анализе функций, представленных полиномами.

Функция FunctionChart может использоваться с многочисленными опциями, существенно влияющими на вид рисунка — рис. 8.74. В данном случае анализируется функция sin(x)/x.

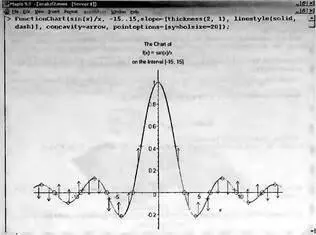
Рис. 8.74. Визуализация функции sin(x)/x

Визуализация функций весьма полезна в учебных целях при детальном изучении свойств той или иной функции.

В ряде случаев обычная техника анимации оказывается не очень подходящей из-за ограничений на выбор опций. Такова, например, ситуация, когда желательно обеспечить анимацию с большим числом кадров сложной поверхности, освещаемой от некоторого источника света. Пример такого рода представлен на рис. 8.75.

Рис. 8.75. Задание поверхности — мембраны

На рис. 8.76 задана упругая поверхность мембраны, закрепленной по периметру. Мембрана имеет ряд выпуклостей и впадин, переходящих друг в друга. Начальный вид мембраны представлен на рис. 8.76. Там же показано контекстное меню мыши, с помощью которой можно запустить анимацию — в том числе по кадрам.

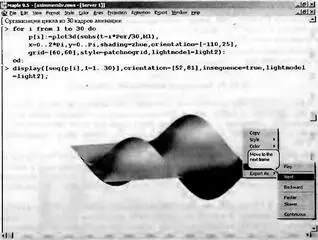
Рис. 8.76. Организация анимации мембраны и ее начальное положение

А на рис. 8.77 представлен промежуточный кадр анимации, из которого хорошо виден ее характер. В частности, выпуклости мембраны переходят во впадины и наоборот. С учетом выбранной схемы освещения мембраны ее колебания выглядят очень эффектно и наглядно, что особенно ценно при использовании подобных примеров в образовании.

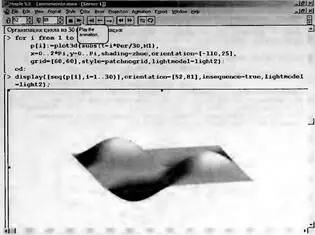
Рис. 8.77. Промежуточный кадр анимации поверхности мембраны

Различные поля (электрические, гидравлические, гравитационные и иные) относятся к достаточно сложным понятиям, визуализация которых представляет значительные трудности в связи с большим объемом вычислений параметров поля, выполняемых во многих точках пространства с разными системами координат и отсутствием у людей органов для наблюдения полей.

В пакете VectorCalculus можно найти функции, которые совместно с графикой ряда других пакетов обеспечивают высокую степень визуализации полей с помощью стрелок, направления и размеры которых указывают на количественные оценки полей и изменения их градиентов в различных точках полей. Не вдаваясь в тонкости математической и физической интерпретации таких графических построений, приведем несколько примеров их выполнения, иллюстрирующих возможности рассматриваемого пакета в визуализации полей.

Рисунок 8.78 иллюстрирует поиск трех локальных экстремумом поверхности, представленной функцией двух переменных. Экстремумы — минимумы ищутся с помощью функции fsolve по нулям частных производных по поверхности, вычисляемым функцией cliff пакета VectorCalculus. Это расширяет методы поиска экстремумов функций двух переменных.

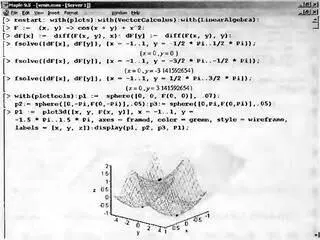
Рис. 8.78. Визуализация поиска локальных минимумов поверхности

В найденных точках минимумов размещены черные сферы, что позволяет наглядно представить положение точек минимума поверхности. Правда, сферы выглядят как эллипсоиды, поскольку при выводе графиков выравнивание масштабов изображения по всем трем осям не предусматривалось.