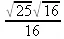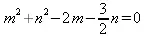Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Учитывал идентичность идеологии при работе с функциями этого пакета, большинство из которых имеет вполне прозрачные имена (правда, англоязычные), работу с пакетом поясним на примере одной из функций — circle. Она позволяет математически задать окружность и определить все ее геометрические параметры. Функция может иметь несколько форм записи. Например, в форме

circle(с, [А, В, С], n, 'centername'=m)

она определяет построение окружности, проходящей через три точки А, В и С. Необязательный параметр n — список с именами координатных осей. Параметр 'centername'=m задает имя центра.

В форме

circle(с, [А, В], n, 'centername'=m)

задается окружность, проходящая через две точки А и В, а в форме

circle(с, [A, rad], n, 'centername'=m)

задается окружность, проходящая через одну точку А с заданным (и произвольным) радиусом rad и центром с. Наконец, функция circle в форме

circle(с, eqn, n, 'centername'=m )

позволяет задать окружность по заданным уравнению eqn и центру с.

Проиллюстрируем применение функции circle на следующих примерах. Зададим характеристические переменные:

> _EnvHorizontalName := m: _EnvVerticalName := n:

Определим окружность с1, проходящую через три заданные точки А, В и С с указанными после их имен координатами и найдем координаты центра этой окружности:

> circle(c1,[point(А,0,0), point(В,2,0),point(С,1,2)], 'centername'=O1):

> center(c1), coordinates(center(c1));

Далее найдем радиус окружности

> radius(c1);

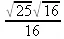
и уравнение окружности, заданное в аналитическом виде:

> Equation(c1);

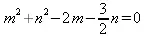
Наконец, с помощью функции detail получим детальное описание окружности:

> detail(c1);

Одно из важных достоинств пакета geometry — возможность наглядной визуализации различных геометрических понятий, например, графической иллюстрации доказательства теорем или геометрических преобразований на плоскости. Проиллюстрируем это на нескольких характерных примерах, заодно показывающих технику работы с рядом функций этого пакета.

Рис. 9.1 показывает построение из множества окружностей фигуры — кардиоиды. Вопреки обычному построению этой фигуры, используется алгоритм случайного (но удовлетворяющего требованиям построения данной фигуры) выбора положений центров и радиусов окружностей.

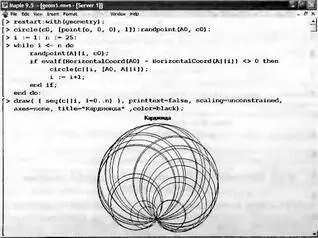
Рис. 9.1. Построение кардиоиды из окружностей

Рис. 9.2 дает графическую иллюстрацию к одной из теорем Фейербаха. Здесь эффектно используются средства выделения геометрических фигур цветом, что, увы, нельзя оценить по книжной чёрно-белой иллюстрации.

Рис. 9.2. Графическая иллюстрация к теореме Фейербаха

На следующем рисунке (рис. 9.3) показано построение фигуры, образованной вращением множества квадратов относительно одной из вершин. Это хороший пример применения функций point, square, rotation и draw из пакета geometry.

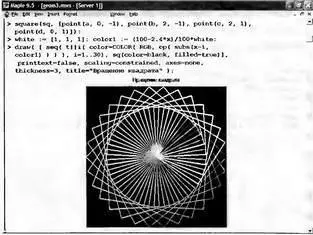
Рис. 9.3. Фигура, полученная вращением квадрата

Рис. 9.4 показывает гомологические преобразования квадрата. Заинтересовавшийся читатель может легко разобраться с деталями простого алгоритма этой программы.

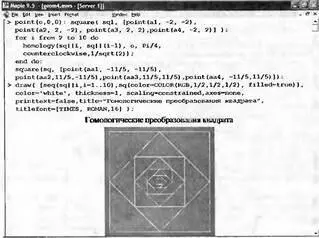
Рис. 9.4. Гомологические преобразования квадрата

Обратите особое внимание на последний параметр в функции draw. Он задает построение титульной надписи с заданными шрифтом и размером символов. Сравните титульные надписи на рис. 9.4 и на рис. 9.3, где титульная надпись сделана шрифтом, выбранным по умолчанию. Приятно, что в обоих случаях нет преград для использования символов кириллицы и создания надписей на русском языке.